Get it on Google Play Get it on Apple Store

LINEAR ALGEBRA NOTES

Contents

1. Systems of linear equations
2. Matrices of a system
3. Gauss elimination
4. Matrices
5. Matrix operations
6. Inverse matrix
7. Determinants
8. Vector spaces
9. Linear independence
10. Bases
11. row, column and null spaces
12. Coordinates
13. Linear transformations
14. Eigenvalues and eigenvectors
15. Diagonalization
16. Bilinear functional
17. Inner product
18. Orthogonal bases and Gram-Schmidt algorithm
19. Least square solution and linear regression

1. Systems of linear equations

linear equation: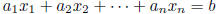

variables: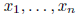
coefficients: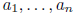
main coefficient: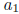
constant term : b

linear system: m equations, n unknowns

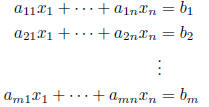
solution: n-tuple 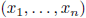satisfying all equations

consistent system: has a solution

inconsistent system: has no solution

solution set: set of all solutions

equivalent systems: have the same solution set

elementary operations on equations : make equivalent systems

(i) multiply an equation by a nonzero constant
(ii) interchange two equations
(iii) add a constant multiple of an equation to another

elimination: use elementary operations to eliminate unknowns

fact: a linear system has no solution, exactly one solution or infinitely many solutions

parameters: used to describe infinitely many solutions

homogeneous system: constant terms are 0 (consistent)

trivial solution: all variables are 0

2. Matrices of a system

coefficient matrix :

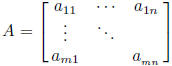
constant vector: 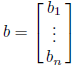unknown vector: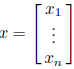

augmented matrix:

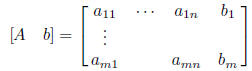
3. Gauss elimination

elementary row operations: (ero) correspond to elementary operations on equations

(i) multiply a row by a nonzero constant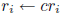
(ii) interchange two rows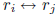
(iii) add a multiple of a row to another row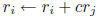

row equivalent matrices: one can be gotten from the other by elementary row operations

fact: linear systems with row equivalent augmented matrices have the same solution set

echelon matrix: the number of leading zeros is strictly increasing in each row until you get all 0 rows

Gauss elimination: use elementary row operations to get echelon form

leading entry: first nonzero entry in a row

leading (pivot) column: column containing a leading entry

leading variable: a variable corresponding to a leading column

free variable: not leading

back substitution: get solution set from echelon form

(i) set free variables equal to parameters
(ii) solve last nonzero equation for leading variable
(iii) substitute into preceding equation
(iv) continue

reduced echelon matrix:

(i) echelon matrix
(ii) every leading entry is 1
(iii) every leading entry is the only nonzero entry in it's column

Gauss-Jordan elimination: use elementary row operations to get reduced echelon form

fact: every matrix is row equivalent to a unique reduced echelon matrix

fact: system with square coefficient matrix A has unique solution i A is row equivalent to I

fact: system with more unknowns than equations is inconsistent or has infinitely many solutions

4. Matrices

matrix: rectangular array of numbers

notation: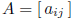

scalar: real number

size of a matrix: size (A) = m × n if m rows and n columns

square matrix: m = n

diagonal matrix: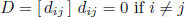

zero matrix : O all entries 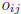are 0
identity matrix: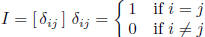

(column) vector: has size n× 1

row vector: has size 1 × n
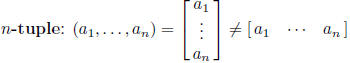slightly abusive
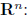set of n-tuples,

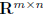: set of m × n matrices, 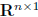is identified with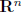

basic unit vectors: 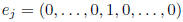(1 in j-th position), column vectors of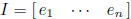

column vectors:

5. Matrix operations

matrix addition: 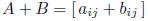  if A, B have the same size

matrix subtraction: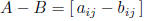

scalar multiplication: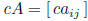

negative matrix : -A = (-1)A

properties:

A + B = B + A commutative
A + (B + C) = (A + B) + C associative
c(A + B) = cA + cB distributive
(c + d)A = cA + dA distributive
(cd)A = c(dA) associative

matrix multiplication: C = AB, size(C) = m × n, size(A) = m × p, size(B) = p× n



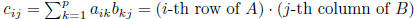
properties:

A(BC) = (AB)C associative
A(B + C) = AB + AC distributive
(A + B)C = AC + BC distributive
c(AB) = (cA)B = A(cB)

warning:

AB ≠ BA in general


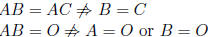
transpos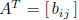e: where

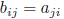
properties:


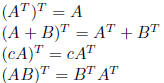
fact: product of diagonal matrices is diagonal

matrix form of linear system: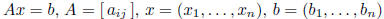
linear combination: of obje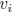cts is a finite sum of scalar multiples of the objects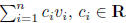
span: of obje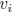cts is the set of linear combinations of the objects

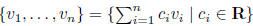
fact: solution set of homogeneous system is the span of particular solutions (one for each parameter)

6. Inverse matrix

A invertible: 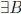such that AB = BA = I

B is the inverse of A (A is also the inverse of B)

properties:

invertible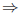 square
inverse is unique if exists, notation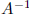



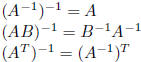
if A is invertible then Ax = b has unique solution
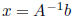
fact: 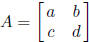is invertible iff 

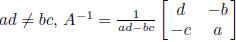
elementary matrix: 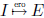single elementary row operation

properties:

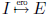implies 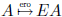equivalently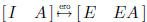
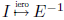  inverse ero

fact: A invertible i A row equivalent to I

fact: A, B row equivalent iff 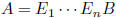 , for 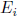elementary

algorithm for A-1: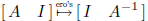
more generally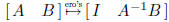

7. Determinants

notation: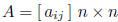



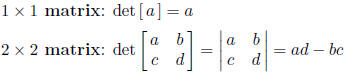
notation: 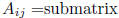after deletion of i-th row and j-th column
ij-th cofactor of A: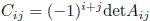

chess board rule:

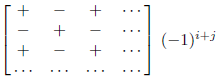
inductive definition: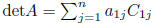
cofactor expansion along first row

cofactor expansion:
along i-th row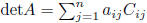
along j-th column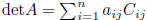

elementary row operations:



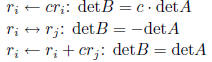
properties:

A triangular implies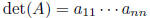
detI = 1
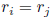implies detA = 0

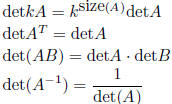
A invertible iff detA ≠ 0

Cramer's rule: detA ≠ 0 implies solution of Ax = b is

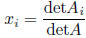where 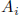comes from A after replacing i-th column by b

adjoint of A: 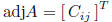transpose of matrix of cofactors
adjoint formula for inverse: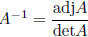

Prev Next