Math Test #1 Review Sheet

Test #1 will be held in the lecture on Monday, September 26, 2005. It will cover §7.1, §7.2, §7.3, §7.4, §7.7, §7.8, and
§8.1. You cannot use a calculator, books, or notes. The test will be 50 minutes long.

This review sheet is intended to help you prepare for the test . It states pretty much what we have done in a nutshell,
but this list is not exhaustive. Please be sure you are familiar with all the concepts listed here. If you’re having trouble,
be sure to stop in at Professor Mackey’s or your TA’s office hours.

There will be a review session held on Sunday, September 25, 2005 from 3:00pm until 4:00pm in Porter Hall 100 (the
large lecture hall). The session will be led by Sunil Raman, the TA for Section H. I highly recommend attending this,
since it will help answer any last-minute questions you may have.

I attached a practice test for you. All but one of the questions came directly from an actual test that was given in the
Fall 2002 semester. Hopefully it will help you study.

§7.1 Integration by Parts

• Integration by parts forumulas:

–Indefinite integrals: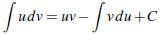

– Definite integrals: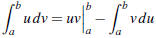

• You want the integral on the right hand side to be easier to solve than the original integral. If it’s harder, chances
are you made the wrong choice for u and dv.

• If the integral on the right hand side is exactly equal to the original, solve for it.

• How to choose u: LIATE

L ogarithmic

I nverse trigonometric functions

A lgebraic (i.e. polynomials, terms under square roots, etc.)

T rigonometric functions

E xponentials

• In all cases, you want u to be easy to differentiate and dv to be easy to integrate.

§7.2 Trigonometric Integrals

• You need to know trigonometric identities to do well in this section.
• If you have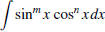

– If n is odd, split off a copy of cosx, let cos² x = 1−sin² x, then let u = sin x.
– If m is odd, split off a copy of sinx, let sin² x = 1−cos² x, then let u = cosx.
– If both powers are even , let

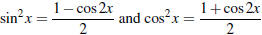
• If you have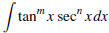

– If n is even, let sec² x = 1+tan² x, then let u = tan x.
– If m is odd, split off a copy of secx tan x, let tan² x = sec² x−1, then let u = sec x.

• Remember that .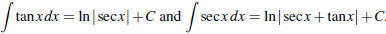
• Don’t be afraid to multiply the integrand by factors like 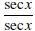or 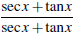. You need to do this when integrating
secx, for example.

• You do NOT need to know the formulas in the box on page 487.

§7.3 Trigonometric Substitution

• You need to know trigonometric identities to do well in this section, too.

• What to substitute:

• Remember to draw a triangle to figure out the values for the other trigonometric functions are.

• Expression not in one of the forms above? Try completing the square and factoring .

• Remember to change the limits if doing a definite integral! If you don’t, you’ll get the wrong answer.

§7.4 Integration by Partial Fractions

• Before trying to use partial fractions, try to simplify : if deg(numerator) ≥ deg(denominator), divide using
polynomial long division.

• Factor all terms in the denominator if possible.

• 4 cases to consider and what to do:
1. Distinct Linear Factors : Split into form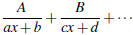
2. Repeated Linear Factors : Split into form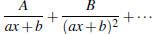
3. Distinct Quadratic Factors : Split into form
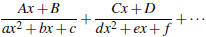
4. Repeated Quadratic Factors: Split into form

• NOTE: The quadratic factors in the latter 2 cases must be irreducible. This will not work if the quadratic
factors are reducible.

• Often you’ll have mixtures of these cases. Just remember to treat each factor in the denominator separately . For
example,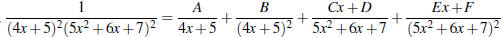

§7.7 Approximate Integration

• You do NOT need to memorize the formulas for the Midpoint Rule, the Trapezoid Rule, and Simpson’s Rule.
You also do not need to memorize the error formulas. All formulas in this section will be given to you on the
test should you need them.

• You DO need to how these formulas arise geometrically.

• Remember that for f (x), if 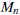is an underestimate of 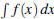, then 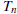is an overestimate of 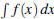, and vice
versa. A lot of people missed this on Homework 3, and you need to know this.

§7.8 Improper Integrals

• How to set them up:

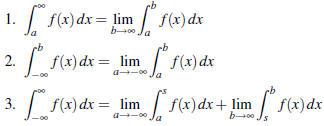
• In the setup above, pick s to be something convenient, like 0.

• If f (x) has a vertical asymptote, split the integral there, and take left and right hand limits.

• If you split an integral and one portion diverges, stop. The integral diverges.

• Remember to carry the limits all the way through. Not doing this will cause you to lose points.

§8.1 Arc Length

• Arc length of f (x) from (a, f (a)) to (b, f (b)) is .

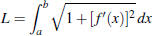• You may need to use Simpson’s Rule or other approximate integration methods if the integrand gets ugly.

This practice test is intended to help you study for Test #1, to be given on Monday, September 26, 2005. All but
one of these questions came from an actual test which was given in the Fall 2002 semester. You should take this test
in a quiet area with all books, notes, and calculators put away and out of sight. You have 50 minutes. There is a total
of 104 points (4 bonus points). The point value is indicated in brackets [ ].

NOTE: This test is (hopefully) more difficult than what you will be given on Monday.

[16] QUESTION 1 Evaluate the indefinite integral 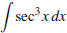Show all your work.

[16] QUESTION 2 Make a substitution to express the integrand below as a rational function and evaluate the resulting
integral. Show all your work.

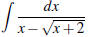
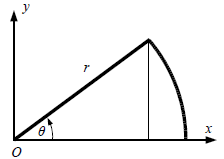
[20] QUESTION 3 Set up and evaluate an expression involving a definite integral to find the formula for the area of a
sector of a circle of radius r and central angle θ. Assume 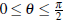and consider a circle whose center is at the origin
as in the diagram below. Show all your work.

[12] QUESTION 4 Evaluate the indefinite integral 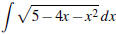. Show all your work.

[8] QUESTION 5 Determine if the improper integral 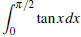converges or diverges. Show all your work.

QUESTION 6 Consider the definite integral .

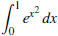[10] PART A Using the Trapezoid Rule formula 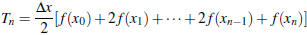, write down (but
do not evaluate) an expression for .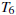

[10] PART B Show how to find the smallest number K such that 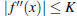on [0,1] and then use the error formula
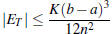to find a value of n for which the error using is within 0.01. (Note to Section D: This was the
question I meant to ask you in recitation last week.)

[12] QUESTION 7 Find the length of the curve y = ln(sec x) such that 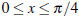. Show all your work.