Finding areas of squares and
other figures by
sub dividing or enclosing : These strategies for
finding areas were developed in Covering and
Surrounding. Students review finding areas by
partitioning the figure into shapes whose areas they
can easily find, or by surrounding the figure with a
rectangle or square and subtracting the “extra” areas.
Note: the reason for this review is to
have students
develop a strategy for finding the length of the side of
a square, if the area CAN be calculated but the
length of a side can NOT be calculated with existing
knowledge.
|
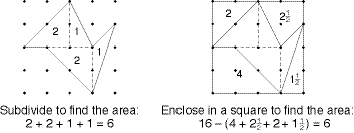
1. In the figure on the left below, the shape is
divided into 4 triangles, the areas of which can
be found by using the given base and height.
(See Covering and Surrounding for area of
triangle.) In the figure on the right the same
shape is surrounded by a square whose edges
are each 4 units, so the square has area 16
square units. We must now subtract the “extra”
areas, some of which are triangles, and some of
which are shapes that can be divided into
squares and triangles.
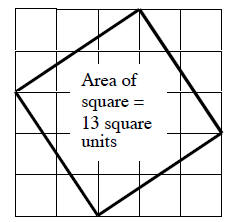
2. The bolded square be low does not “line
up” against the grid lines and so it is hard to
calculate, or see its area. However, if we draw
broken lines, as shown, we can figure out that
the area is actually made of 4 right triangles,
with area 3 square units, and 1 small square
with area 1 square unit. The total area of the
square is 13 square units.
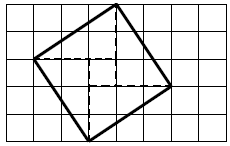
Note: this area could also have been calculated
by surrounding the bolded square with a
rectangle.
|
Square Root: can be thought of
as the length of the
side of a square whose area is known. Thus, a
square with area 9 square units has a side of length
square root of 9, or 3 units. We write “square root of
9” as √9. Or, it can be thought of as a number which
when multiplied by itself gives a target number.
Thus, to evaluate √20 we need to find a number
which when multiplied by itself yields 20.
Benchmarks: are useful when trying to evaluate
square roots. Thus, √20 must be greater than 4,
because 4 is √16, but less than 4, because √25 is 5.
Since many square roots are irrational (see below)
students can not calculate them exactly. They will
either rely on benchmarks, or on a calculator.
|
3.
Area of bolded square = Area of outer square –
4 triangles
= 9 square units – 4(1) square units
= 5 square units
So length of side of square = √5 units.
4.
2 x 2 = 4
3 x 3 = 9
The area of the bolded square below is 5
square units (see example 3). So each side
has length √5 units.
? x? = 5
Since 4 < 5 < 9, taking square roots, 2 < √5 < 3.
Comparing the areas of the square figures
above, we would guess that√5 is closer to 2
that to 3. Students might guess and check,
using calculators or multiplying by hand. 2.1 x
2.1 = 4.41, 2.2 x 2.2 = 4.84, 2.3 x 2.3 = 5.29.
Apparently √5 is between 2.2 and 2.3. (Using a
calculator we find that √5 is approximately
2.236. √5 is irrational, so there is no exact
terminating decimal equal to √5.) |
The relationship between square
area and side
length: Since the side length of a square is the
square root of the area of a square, students can find
areas, using partitioning or surrounding strategies,
and then use this to find the side length..
|
5.
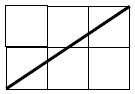
The length of the above line segment could be
measured with a ruler ; since all measurement is
an approximation this would give us some idea
of the length. To calculate an exact length,
as suming the line segment connects two
vertices on the grid, we could construct a
square on this line segment, find the area of the
square (using partitioning or surrounding as a
strategy) and then calculate the length of a side.
So length of side of square = exactly √13, or
approximately 3.6 units. |
Pythagoras Theorem: says that
the sum of the
square areas on the two shorter sides of a right
triangle is the same as the area on the longest side
(hypotenuse) of the right triangle.
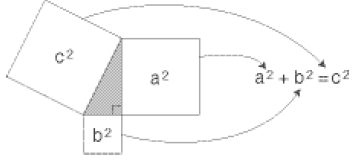
Students discover this pattern when they build
squares on the sides of a right triangle, and then find
the areas as in example 5 above. They also
investigate a proof that this pattern works for all right
triangles, and only for right triangles.
The converse of the Pythagoras Theorem
states
that if the sum of the areas of the squares on the two
shorter sides of a triangle is the same as the square
area on the longest side of the triangle, then the
triangle must be a right triangle. Note that the
original theorem starts with a given right triangle and
proves the relationship between the square areas.
The converse starts with the given relationship
between the square areas and proves the triangle
must be right angled.
Pythagorean Triples: are sets of three
whole
numbers that fit the Pythagorean relationship, and
therefore form right triangles. For example, 3 – 4 – 5
is a Pythagorean Triple, because 32 + 42 = 52.
Therefore we can form a right triangle with these
lengths or with any scaled up copy (see Comparing
and Scaling) of these lengths. The triple 3 – 4 – 5 is
really a ratio 3:4:5, since any multiple of 3 – 4 – 5 will
also be a Pythagorean Triple. In fact all right
triangles formed by the triple 3 – 4 – 5 will be similar.
There is an infinite number of these Pythagorean
Triples. 5:12:13 is another example.
|
6.
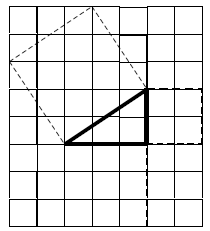
The original triangle has sides 2, 3 and a
hypotenuse of unknown length . The areas of
the squares on the sides are 4 and 9 square
units. The area of the square on the
hypotenuse can be calculated as in example 5,
13 square units. For this example we can see
that the sum of the areas of the squares on the
two sides of a right triangle (4 + 9 square units)
is the same as the area of the square on the
hypotenuse (13 square units). Note: This is
only one example , and should not be regarded
as a proof. Students do a very visual proof
using an arrangement of triangles and squares
to show that the sum of the square areas on the
short sides of any right triangle is the same as
the area of the square on the hypotenuse..
7. Is the following triangle right angled?
Lengths of sides are a = 2.5, b = 6 and c = 6.5
units.
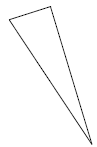
We could measure all the angles in the triangle,
but this would be an approximation of angle
sizes. We can calculate squares of side lengths
as follows:
a 2 = 2.52 = 6.25.
b 2 = 62 = 36.
c2 = 6.52 = 42.25.
Since a2 + b2 = c2 we can deduce that this
triangle is right angled, with the right angle
opposite the longest side, c.
8. Find the distance between two points on a
coordinate grid .
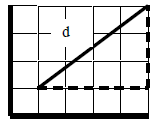
The above sketch shows a line segment joining
two points on a coordinate grid. The points are
(1, 1) and (5, 4). To find the distance between
these two points we can create a right triangle,
and apply the Pythagorean Theorem.
d2 = 32 + 42 = 25. Therefore, d = 5.
|












