Math 107 Test 2
READ ALL DIRECTIONS CAREFULLY:
- Turn o and put away all cell phones, pagers, iPods, cd players, etc.
-Write your name, test version, and row number on the outside of your blue book.
-Write ALL work and answers in your blue book - we will NOT look for, or grade,
work on the test sheet.
-You must SHOW ALL WORK for full credit.
-When you are finished, fold your test so that it fits inside your blue book and
turn
in the test and blue book.
1. (20 Points) The price, p, in dollars, and the quantity, x, sold of a
certain product obey the
demand equation below :
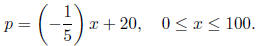
(a) Express the revenue R as a function of x.
(b) What quantity maximizes revenue?
(c) What is the maximum revenue?
(d) What price should the company charge to maximize revenue?
2. (10 Points) A farmer with 6000 meters of fencing wants to enclose a
rectangular plot split in
two that borders on a river. The farmer does not fence the side along the river.
Express the area
A of the rectangle as a function of x.
Things we know: A = xy and P = 3x + y = 6000
So we can solve for y in terms of x using the perimeter and get y = 6000 - 3x.
Then we plug this
in to our equation for A.
A = xy = x(6000 - 3x) = 6000x - 3x^2
3. (20 Points) Given the following polynomial
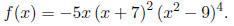
(a) What is the degree of the function?
(b) List each real zero , its multiplicity, and whether the graph crosses or
touches the x-axis at
each zero. Write it in a form similar to the chart below. (Hint: The
multiplicities add up to the degree.)
| zero | multiplicity | graph behavior |
(c) Find the power function that the graph of f(x) resembles for large values of |x|.
(a) The degree is 11.
| zero | multiplicity | graph behavior |
| 0 -7 3 -3 |
1 2 4 4 |
cross touch touch touch |
(c) f(x) resembles -5x11 for large values of |x|.
4. (12 Points) Given the following rational function:
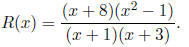
(a) What is the domain of R(x)?
(b) Find any vertical asymptotes or holes. Show work to justify your answer.
(c) Find any horizontal asymptotes. Show work to justify your answer.
(a) Domain: All reals except x = -1 and x = -3.
Know because Red Flag! Cannot have 0 in the denominator.
(b) VA or holes:
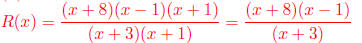
So, there is a hole at x = -1 and VA at x = -3.
(c) Degree of the numerator is 3 and degree of the denominator is 2, so we do
not have a HA.
5. (12 Points) Solve this inequality algebraically :
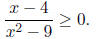
Step One : done
Step Two: Since the function can be factored to be
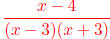 we see that we have VAs at
we see that we have VAs at
x = 3 and x = -3 and a zero at x = 4.
Steps Three and Four: We can see that our intervals are
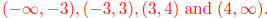 Thus
Thus
we pick test points in each interval and check whether the value of f at these
points are positive
or negative .
The answer is that 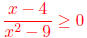 when x is in [-3, 3] or x is in
when x is in [-3, 3] or x is in 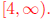
6. (10 Points) Given the following function:
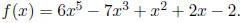
(a) List all potential rational zeros.
(b) Use synthetic division to find the quotient and remainder when f(x) is
divided by (x - 1).
Write f(x) in the form f(x) = (x - 1)*quotient + remainder.
(c) What conclusions can you make about (x-1)? What conclusion can you make
about x = 1?
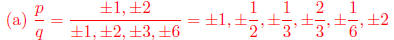
(b) Using synthetic division, we find
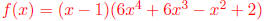
(c) (x - 1) is a factor of f(x) and x = 1 is a root /zero/x-intercept of f(x).
7. (5 Points) What is the remainder if
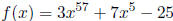 is divided by (x - 1)?
is divided by (x - 1)?
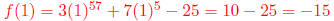
8. (5 Points) Write the equation (make one up) of a rational function that has a horizontal asymptote at y = 0.
Any function where the degree on the bottom is more than the degree on top will work.
9. (6 Points) Given f(x) = -4x^2 + 5x - 2:
(a) Does this f(x) have a maximum or a minimum? How do you
know?
(b) Where does the maximum or minimum occur and what is its value?
(a) f(x) has a maximum because a is negative, so the
parabola opens downward.
(b) This maximum occurs at the vertex , so it occurs when x = 5/8 and the maximum
value is f(5/8) = -.4375.
| Prev | Next |