MATH 110 CHAPTER 3 NOTES
Rational Zero Theorem :
If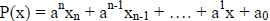 
has integer coefficients and
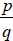is a rational zero
(in lowest terms ) of P,
then
• p is a factor of the constant term a 0 and
• q is a factor of the leading coefficient a n
Examples - continued:
Find the possible rational zeroes of the polynomial functions .
1. P(x) = 3x3 + 11x2 – 6x – 8
2. P(x) = 2x4 – x3 + 2x2 + 1
Examples:
1. Find the zeroes and sketch the polynomial function P(x) = 2x3 - 3x2 - 3x + 2.
2. Find the zeroes and sketch the polynomial P(x) = 3x4 - 2x3 - 25x2 + 28x + 12.
Homework: pg. 321 # 1, 3, 7, 9, 11, 27, 29, 35, 41, 43, 55
The Fundamental Theorem of Algebra :
Complex Numbers (a + bi)
• The Real Numbers are a subset of the Complex Numbers
Examples of Complex Numbers:
Examples of Real Numbers:
The number of zeros of a polynomial function:
If P(x) is a polynomial function of degree n ≥ 1, then P(x) has exactly n
complex zeros,
provided each zero is counted according to multiplicity .
Example:
How many complex zeros does the function have?
F(x) = x5 – x4 + 3x2 – 1
Examples:
Find the zeros and linear factors of the following polynomial functions.
1. P(x) = x3 – 13x2 + 65x – 125
2. P(x) = x5 + 2x4 - 4x3 - 12x2 + 3x + 10
3. P(x) = x5 – 9x4 + 34x3 – 58x2 + 45x – 13
Examples:
Find a polynomial that has the following zeros:
1. 2, -2, 1
2. 2i, 7
Homework: pg. 332 # 1, 3, 5, 9, 13, 37, 39, 40
Graphs of Rational Functions and their Applications:
Consider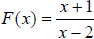 
Find the x- and y-intercepts.
Find the domain (set the denominator equal to zero).
Sketch the graph based on this information.
Vertical Asymptote:
The line x = a is a vertical asymptote of the graph of the function F provided
F(x) → ∞ or F(x) → -∞
as x approaches a from either the left or right.
Graphs:
Horizontal Asymptote:
The line y = b is a horizontal asymptote of the graph of a function F provided
F(x) → b as x → ∞ or x → -∞
Graphs:
Theorem of Vertical Asymptotes:
If the real number a is a zero of the denominator Q(x), then the graph of
F(x)=P(x)/Q(x),
where P(x) and Q(x) have no common factors , has the vertical
asymptote x = a.
Theorem on Horizontal Asymptotes:
Let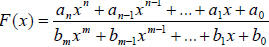 
be a rational function with numerator
of degree
n and denominator of degree m.
1. If n < m, then the x-axis, which is the line given by y=0, is the horizontal
asymptote of the graph of F.
2. If n = m, then the line given by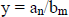 
is the horizontal asymptote of the
graph
of F.
3. In n > m, then the graph has no horizontal asymptotes.
Example:
Find the vertical and horizontal asymptotes of each function.
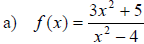
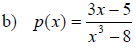
General Procedure for Graphing Rational Functions that
have no Common Factors:
Let F(x) = P(x)/Q(x)
1. Asymptotes
Find the real zeros of the denominator Q(x). For each zero a, draw the dashed
line
x = a. Each line is a vertical asymptote of the graph of F. Also graph any
horizontal asymptotes.
2. Intercepts
Find the real zeros of the numerator P(x). For each real zero c, plot the point
(c,0).
Each such point is an x- intercept of the graph of F. For each x-intercept
use the
even and odd powers of (x-c) to determine if the graph crosses the
x-axis at the
intercept of if the graph intersects but does not cross the
x-axis. Also evaluate
F(0). Plot (0,F(0), the y-intercept of the graph of F.
3. Complete the sketch.
Use all the information obtained above to sketch the graph of F.
Example:
Sketch the graph of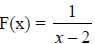 
Example:
Sketch the graph of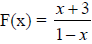 
Example:
Sketch the graph of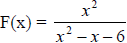 
Homework: pg. 348 #1, 3, 5, 7, 9, 15, 17, 21, 23, 25, 27, 29, 31, 33
| Prev | Next |