MATH 128 TEST 2 SAMPLE

1.) Twelve-hundred feet of fencing is available to enclose a rectangular playground and subdivide it into two smaller rectangular regions. One side of the playground is along the school building wall and requires no fencing as shown below. What is the maximum area that can be enclosed?

2.) Divide and write in standard form:

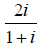
3.) ( 15 points) Graph 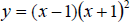Find the intercepts and multiplicities , and behavior at each zero (what equation the graph resembles at each zero), max. number of turning pts, degree.

zero:_______ Multiplicity :_______ Behavior at zero:_________________
zero:_______ Multiplicity:_______ Behavior at zero:_________________
y-int:______________ Degree:__________ Max turning pts:___________

4.) (10 points) Use the following equation to answer the below questions:

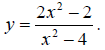
4a.) Find the intercepts.
x-int:___________________
y-int:___________________
4b.) Find the asymptotes.
Vertical:_________________
Horizontal:______________
4c. Graph.

5.) (15 points) Given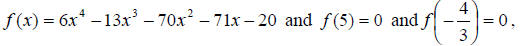

answer the following:

a.) Use Descartes’ Rule of Signs to find the number
possible positive and negative zeros .
positive:_________________
negative:________________

b.) Use the Rational Zero Theorem to find the
list of possible zeros.
b._______________________________

c.) Use synthetic division to find the other zeros.
c.______________________

6.) Solve and write in interval notation:

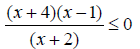
7.) (10 points) Use the given zero to find the other zeros:

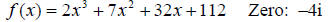
8.) Graph 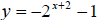(Please use dotted lines to show new  set of axis.)

9.) Find the exact value using log properties (your answer should NOT contain logs):

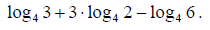
10.) Expand and write without exponents:

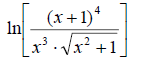
11.) Solve:

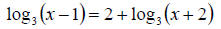
12.) Krypton-91, an isotope, has a half-life of 10 seconds.
How much of a 3 gram sample remains after 16 seconds?

13.) Las Vegas began with 2 Dunkin Donuts stores. It is estimated that 2.25 years later there will
be 14 stores.

a.) Find the exponential growth function that describes
the given information.

13a.____________________

b.) How many stores are estimated to be in Las Vegas
after 3.5 years? (Round to the nearest whole number )

13b.____________________

14.) Solve the system : 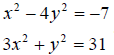Write answer as ordered pairs .