Math 5126 Second Test Review

Solution to Problem 1 on Sample Test no. 1 We are working in the group of units of
(Z/625Z)^x, which is a cyclic group of order θ(625) = 500. Since x⁵⁵⁰ x⁵⁰ mod 625,
we need to prove that 499¹⁰ 1 mod 625, equivalently 126¹⁰1 mod 625. However
126⁵ (1+5³)⁵ 1 mod 5⁴ and the result follows.

Solution to Problem 2 on Sample Test no. 1 Write the primes not equal to the characteristic
p of K as p₁, p₂, . . . (an infinite number of primes). For each i, let K_i be an extension
of degree p_i and let α_i∈ K_i−K. Then [K(α₁, . . . ,α_n) : K] = p₁ . . . p_n, which is not divisible
by p. Therefore K(α₁, . . . ,α_n) is a finite separable extension of K and hence is generated by
a single element, say α. Since the minimal polynomial of α over K is irreducible of degree
p₁ . . . p_n, the result is proven.

Solution to Problem 3 on Sample Test no. 1

(a) The roots of f are 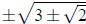. Since the product of all the roots of f is 7, if the product
of two of the roots is a rational number, then so is the product of the other two roots.
Therefore if the product of two of the roots is a rational number , we may assume that
one of the roots  is 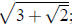then we can just go through the three possibilities for the
other root and check that the resulting product is not a rational number .

Now suppose f is not irreducible. Clearly it does not have a linear factor , so the only
possibility is that it is the product of two quadratic factors ; let g ∈ Q[x] be one of these
factors . Then the constant coefficient of g is the product of the roots of g, consequently
the product of two of the roots of f is a rational number, which contradicts the previous
paragraph.

(b) Suppose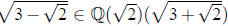. Since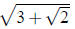satisfies a quadratic over
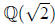we may writ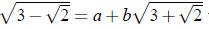e where 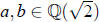. Squaring , we
obtain

.

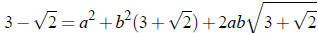From (a), we see that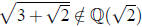 and we deduce that either a or b = 0. Clearly
we can’t have b = 0 (otherwise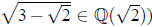 , so a = 0 and we deduce that
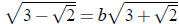with 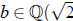). Multiplying both sides by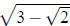, we conclude
that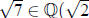), which is not the case. This contradiction finishes the proof of
(b).

(c) Since f has degree 4, its Galois group G will be isomorphic to a subgroup of S₄. Also
we see from (b) that the splitting field of f has degree 8 over Q. We conclude that G
is isomorphic to a subgroup of order 8 in S ₄. Since 8 is the order of a Sylow subgroup
of S₄, there is only one such group up to isomorphism (any two Sylow subgroups are
conjugate), and such a group is nonabelian (in fact isomorphic to D₈).

Solution to Problem 1 on Sample Test no. 2 The only way for there to be a proper
intermediate field is the case f is irreducible, and then [Q(α) : Q] = 4. Suppose K is a
proper subfield, so [K : Q] = 2, and let g denote the minimal polynomial of α over K. Then
g is of the form (x−α) (x− β), where β is one of the other 3 roots of f . If β is complex,
then so are the coefficients of g in degrees 0 and 1, which means that they cannot be in K,
because K ⊆R. We deduce that there is at most one choice for β, namely the other real
root. Since K is generated over Q by the coefficients of g, we conclude that there is at most
one possibility for K and the result follows.

Solution to Problem 2 on Sample Test no. 2 Let K be the splitting field of xⁿ −x over
F_p. Then K = F_n, every element of K satisfies xⁿ −x, and K has degree q over F_p. Let
a∈K−F_p and let f denote the minimal polynomial of α over F_p. Then f has degree q and
divides x ⁿ −x, because α satisfies xⁿ −x. Thus f is an irreducible polynomial of degree q
which divides xⁿ−x, as required.

Solution to Problem 3 on Sample Test no. 2 Let f (x) = x⁵+5x³ −20x+5 and let G
denote the Galois group of f over Q. Note that f is irreducible over Q by Eisenstein for the
prime 5, so all the roots of f are distinct. As x→−∞, f (x)→−∞, and as x→∞, f (x)→∞.
Also f (−1) = 19 and f (1) = −9, which shows that f has a least 3 real roots. Moreover
f '(x) = 5x⁴+15x²−20 = 5(x²+4)(x²−1), consequently f has only 2 turning points and
we deduce that f has exactly 3 real roots . Thus complex conjugation is an element of G
which fixes 3 of the roots of f and interchanges the other 2. Thus when we consider G
as a subgroup of S₅ (i.e. a permutation group on the 5 roots of f ), it has a transposition.
Furthermore 5 | |G| because f is irreducible of degree 5, hence G contains a 5-cycle. Since
S₅ is generated by any transposition and any 5-cycle, we deduce that G ≅ S₅.

Solution to Problem 1 on Sample Test no. 3

(a) Since K^x is cyclic, it is generated by a single element, which we will call α. Then
certainly K = F(α), and if n is the order of α, then αⁿ = 1 and in particular αⁿ ∈ F.

(b) No. One way to see this is that the pth power map π defined by π(k) = k^p is an automorphism
of K, because K is a finite field of characteristic p. Since π(F)⊆ F, we
deduce that π(F) = F and hence π(a) ∉ F for all α ∉ F.

Test on Wednesday, April 2.
Material most of sections 14.1–14.7
One of the problems will be identical to one of the ungraded homework problems and one
of the problems will be identical to one of the sample test problems.