Math 180, problem set #8
(1) There is a rational number r , with denominator less than 50, whose
decimal
expansion begins 1.2941176470588 . . .. Express r as a fraction . (You may need
to use a calculator to compute a continued fraction.)
(2) Suppose x > 0 and x has the continued fraction expansion [a0, a1, a2,
. . .].
What is the continued fraction of 1/x ? (If you can't see the answer, try some
experiments.)
(3) Suppose r is a rational number . Show that there are only
finitely many
rational
numbers m/n (with m, n ∈Z) such that
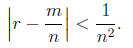
(4) Suppose r is an irrational number . Show that there are
infinitely many rational
numbers m/n (with m, n ∈Z) such that
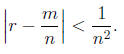
For the next three problems an RSA cipher is set up with
modulus N = 12091 =
107 113 and encryption exponent e = 3.
(5) Encrypt the message 2107.
(6) What is the decryption exponent ?
(7) Suppose the encrypted message (ciphertext) received is 9812. Decrypt it.
In the Diffie-Hellman key exchange, Alice and Bob (being
computationally challenged)
agree to use the prime modulus 101 and the primitive root 2. Alice chooses the
secret
exponent 20 and Bob chooses the secret exponent 41.
(8) What does Alice send to Bob?
(9) What does Bob send to Alice?
(10) What is the shared secret?
| Prev | Next |