Master of Arts in Teaching (MAT)
0! = 1
The fact that 0! = 1 is a useful convention in probability. The number of ways
to arrange
N distinct objects is given by N! and it is a convention to say that there is
only one way to
arrange zero objects . 1! equals 1 is also a useful convention in probability, it
makes sense to say
that there is only one way to arrange 1 object. Using something called the Gamma
Function I
could find an approximation for 3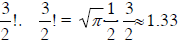 . I do not
believe that there is a
. I do not
believe that there is a
number such that x! = 0 because after learning how to find (1.5!) no matter how
small the
fraction or decimal is it will not become zero. This is similar to the idea of
limits in Calculus.
The Difference Between No Slope and a Zero Slope
Students sometimes have difficulty understanding the meaning of the number zero
in the
context of slope, they may have a hard time determining if the slope of the line
is zero or if the
line is undefined (i.e. has no slope). I explain to the students the difference
between zero slope
and no slope by talking about a “skier dude” in Colorado. In this example I draw
skier dude
skiing on a horizontal line and note that skier dude would say (in reference to
the slope) "this is a
total zero dude." Thus a horizontal line has a slope of zero. Then I draw a
vertical line on the
board with skier dude next to the top of the vertical line and ask what skier
dude would say about
this ski slope. By noting that skier dude would say "oh, no" (because there
would be no way of
surviving the slope), I make the connection that a vertical line has no slope.
During this lesson I
also tie together the previous knowledge of being able to have a zero in the
numerator but not in
the denominator with the slope formula of rise over run. This seems to help the
students
understand slope a little better.
The Angle of Zero Degrees
It can be difficult for some geometry instructors to understand why there is
such a thing
as a zero-degree angle. It is possible that the difficulty lies in their
understanding of the
definition of an angle; that an angle is formed when two rays share a common
endpoint. In a
zero-degree angle, according to this definition, one ray is directly on top of
(coincidental with)
another ray; so some may consider that to just be one ray, and therefore not an
angle at all. Other
instructors may believe an angle is defined as the space between two rays ( with
a common
endpoint), and since there is no space between the rays in a zero-degree angle,
there is no angle
formed. These same difficulties may arise when studying a 360-degree angle.
Similarly, it can
also be difficult for some to understand an angle of 180 degrees, since two rays
which share a
vertex and go in opposite directions form a straight line and no longer appear
to be two rays.
The fact that a protractor has a measure of zero on it provides evidence that
there is such a thing
as a zero-degree angle. A practical example of one can be considered in the
firing of a projectile
from one building to the top of another building with the same exact elevation.
Discounting any
effects from wind or gravity, the angle at which the projectile is fired would
be equal to zero
degrees.
Zero as a Number
The natural numbers are the numbers that are first learned when a child is
growing up.
They consist of the infinite set {1, 2, 3, ….}. I tell my students that they are
the numbers that
come naturally to them, like when they were learning to count on “Sesame
Street”. The natural
numbers are closed under addition. This means that when you add two natural
numbers you get
another natural number. The same rule applies when you are multiplying two
natural numbers.
We can extend the natural numbers to the set of whole numbers by including zero.
The set of
whole numbers is also closed under addition and multiplication. Whole numbers
also include the
zero-multiplication property; specifically when you multiply a natural number by
zero we get
zero for an answer. To explain this first of all it has to be understood that,
when applied to whole
numbers, multiplication is repeated addition. For example 4 * 3 is the same as 4
+ 4 + 4. When
you multiply 5 * 0 you can change it to 0 * 5 by using the commutative property
of
multiplication. The expression 0 * 5 expands to 0 + 0 + 0 + 0 + 0 which has a
sum of zero.
Since these steps will always work when you replace 5 with any whole number, we
see that any
whole number multiplied by zero will give you zero for an answer.
A general proof, assuming the additive property of zero, follows:
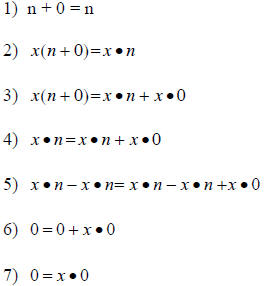 |
Given, by the addition property of zero |
| Multiplication Property of Equality | |
| Distributive Property of Equality | |
| Transitive Property of Equality (steps 2 and 3) | |
| Subtraction Property of Equality | |
| Subtraction | |
| Addition property of zero |
Thus the addition property of zero determines the multiplicative property of zero.
"Proof " that 0 = 1
If a person does not understand all of the rules about using the number zero
some very
strange statements in Algebra can be “proved”. For example here is a proof that
0 = 1which
results from a lack of understanding of the properties about the number zero:
| Let x = 0 | [Given] |
| Then x ( x -1) = 0 | [Multiplication property of 0] |
| Therefore x – 1 = 0 | [Divide both sides by x; Cancellation property] |
| And x = 1 | [Adding 1 to each side of the equation ] |
| Therefore, 0 = 1. |
This “proof” violates a very important property: that
division by zero is undefined. Notice that
to arrive at step 3 from step 2, you have to divide by x, but since x = 0, this
is equivalent to
dividing by zero. Thus the argument is invalid.
Given that a and b are integers such that a = b, prove 0 = 2.
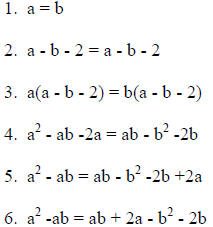 |
1.Given |
|
2.Reflexive Property of Equality |
|
|
3. Multiplication Property of Equality |
|
|
4. Distributive Property |
|
|
5. Addition Property of Equality |
|
|
6. Associative Property of Equality |
|
| 7. a(a - b) = a(b + 2) -b(b + 2) | 7. Distributive Property |
| 8. a(a - b) = (a - b) (b + 2) | 8. Distributive Property |
| 9. a = b + 2 | 9. Division Property of Equality |
| 10. b = b + 2 | 10. Transitive Property (steps 1, 9) |
| 11. Therefore 0 = 2 | 11. Subtraction Property of Equality |
In this "proof" the error is dividing by (a - b) between
steps 8 and 9. The reason this is incorrect
is since a = b, which was the given information, then a - b = 0. Thus the
argument is incorrect.
The Zero Metaphor
There are many metaphors in society which use the word zero. One example is the
"zerobalanced
budget". This is a philosophy in business or in government where the amount of
money taken in should be the same as the amount of money being spent. This is a
concept that is
very hard for groups like local and national governments to achieve; thus the
big deficit we have
here in the United States.
Another metaphor using the number zero is "Ground Zero". This means that an
observer
is at distance zero from a blast site, a phrase which was coined during the
first atom bomb test in
1946. It would be interesting to find out why the Lincoln Journal Star calls
their Friday
entertainment section of the newspaper "Ground Zero" since there is no obvious
connection
between entertainment and the explosion of an atomic bomb.
In the context of measuring temperature, scientists use "absolute zero" to
identify the
temperature at which molecules stop moving. Although a temperature of absolute
zero has never
been achieved, temperatures very close to it have been reached in laboratories.
A website called "The School of Wisdom", indicates the
geometrical representation for
zero-dimensional object is a point. It is only a representation because
physically it is impossible
to draw a point with no length or width.
According to a train of thought called Tao, “The Zero Dimension is the point,
the
infinitely small place holder. It exists not in space, but in time only. It is
the moment between
past and future, the subject, zero.” An article describing the Tao philosophy
also stated that the
Zero Dimension is the home of the natural numbers and the subject point, zero,
is pure
awareness.
Conclusion
The number zero is a very powerful tool in mathematics which has many different
applications and rules. I have learned many truly amazing ways to think about
and work with
zero from writing this paper. I never realized how many different rules there
were for the
number zero in mathematics. This helped me realize why I have to be very careful
in my
teaching when the number zero is involved in the lesson. The number zero is a
very special
number which is much more important and powerful than what its name is
associated with in our
society.
| Prev | Next |