GREATEST COMMON FACTOR
1) A number that divides another number evenly is called a
factor of that number . For example, 16
can be divided evenly by 1, 2, 4, 8, and 16. So the numbers 1, 2, 4, 8, and 16
are called factors of
16. To find the factors of a number, begin with 1 and the number itself, then
divide the number by
2, 3, 4, etc., taking only pairs of factors that divide the number evenly. Stop
when the factors start
to repeat.
2) A number that divides a given set of numbers is called
a common factor of the numbers. For
example, if we list the factors of 16 and 24, we can see these numbers share
common factors of 1,
2, 4, and 8. The greatest common factor (GCF) is the largest common factor that
the numbers
share. Here, 8 is the largest common factor of 16 and 24. So the GCF of 16 and
24 is 8.
Factors of 16 : 1, 2, 4, 8, 16
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
To find the GCF of a given set of numbers, list the
factors of each number to find their greatest
common factor.
3) The GCF of two or more variable terms is the lowest
power of any variables common to each term.
For example, the GCF of the terms x 3yz and x2x2 is x2y because the terms share
common factors of
x2 and y, as shown.
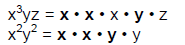
4) To factor a polynomial expression , such as 24x3yz 16x2x2
a) Begin by finding the GCF of the terms of the
expression . For the expression 24x3yz 16x2x2,
the GCF is 8x2y, because 8 is the gcf of the coefficients and x2y is the gcf of
the variables.
b) Next, divide each term of the expression by the GCF .
For example, to factor 24x3yz 16x2x2,
divide each term by 8x2y:
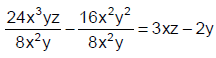
c) Then use the distributive property to write the
expression as a product of the GCF 8x2y and the
quotient of the terms: 3xz 2y:
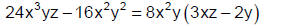
4) In general, to factor out the GCF from a polynomial expression,
a) Find the GCF of the terms of the polynomial.
b) Divide each term of the polynomial by the GCF.
c) Use the distributive property to write the polynomial as a product of the GCF
and the quotient
of the terms.
| Prev | Next |