Matrices, Vectors and Systems of Linear Equations
§1.1 Matrices and Vectors
I Matrices
Definition 1. A matrix is a rectangular array of scalars. If the matrix
has m rows and
n columns, we say that the size of the matrix is m by n, written m × n.
The matrix is
square if m = n. The scalar in the ith row and jth column is called the
(i, j)-entry of
the matrix.
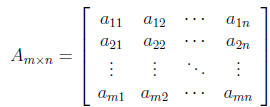
Remark 1.
(i) Two matrices A and B are equal if they have the same size and
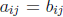for all i
and j.
(ii) If A and B are m × n matrices and c is a scalar, then
• A± B is the m × n matrix with the (i, j)-entry=
.
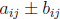• cA is the m × n matrix with the (i, j)-entry= caij .
• The transpose AT of A is the n×m matrix with the (i, j)-entry= the (j, i)-entry
of A, that is,
.
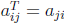(iii) Special matrices:
• Zero matrix 0 is the matrix with each entry= 0.
• The n × n identity matrix is the matrix with the diagonal entry= 1 and the
rest of entries are zero.
Theorem 1. Properties of Matrix Addition and Scalar Multiplication
Let A, B and C be m × n matrices, and let s and t be any scalars. Then
(a) A + B = B + A. (commutative law of matrix addition)
(b) (A + B) + C = A + (B + C). (associative law of matrix addition )
(c) A + 0 = A.
(d) A + (-A) = 0.
(e) (st)A = s(tA).
(f) s(A + B) = sA + sB.
(g) (s + t)A) = sA + tA.
Theorem 2. Properties of the Transpose
Let A and B be m × n matrices, and let s be any scalars. Then
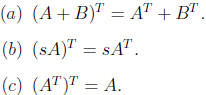
II Vectors
A matrix that has exactly one row is called a row vector and a matrix that has
exactly
one column is called a column vector. The entries of a vector are called
components.
Remark 2. Geometrical interpretation of vectors are explain in the textbook,
page 8-11.
§1.2 Linear Combinations, Matrix-Vector Products and Special
Matrices
III Linear Combinations
Definition 2. A linear combination of vectors
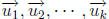is a vector
of the form
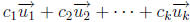
where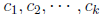 
are scalars. These scalars are called the
coefficients of
the linear
combination .
Remark 3.
(i) In general, the standard vector of Rn is defined by
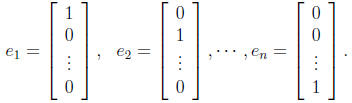
(ii) If 
and
are any nonparallel vector in R2, then
every vector in R2 is a linear
combination of and
.
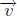IV Matrix- Vector Products
Definition 3. Let A be an m × n matrix and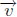 
be an n × 1 vector. We define the
matrix-vector-product of A and 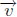, denoted by A 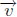, to be the linear
combination of
the column of A whose coefficients are the corresponding components of
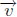. That
is,
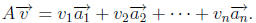
Theorem 3. Properties of Matrix- Vector Products
Let A, B and C be m × n matrices, and let
and
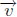be vectors in Rn. Then
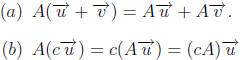for every scalar c.
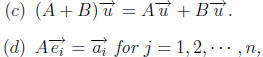where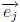 
is the jth standard vector
in Rn.
(e) If B is an m × n matrix such that 
for all
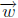in Rn, then B = A.
(f)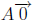 
is m × 1 zero vector .
(g) If 0 is the m × n zero matrix, then 0 is the m × 1 zero vector.
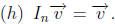
Remark 4. If follows from (a) and (b) in the above theorem, that for any m × n
matrix
A, any scalars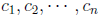 
and any vector
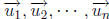in Rn,
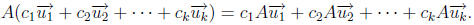
V Rotation Matrices in R2
Definition 4. In R2, we call
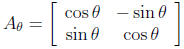
the θ-rotation matrix, or more simply , a rotation matrix.
Remark 5.
1. For any vector in R2, the vector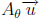 
is the vector obtained by rotating
by
an angle θ, where the rotation is counterclockwise if θ > 0 and clockwise if
θ <
0.
2. The 00-rotation matrix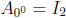 
.
| Prev | Next |