Matrix

Matrices

An m×n matrix is a rectangular array of complex or real
numbers arranged in m rows and n columns:

Types, Operations, etc.

▪ Types: square, symmetric, diagonal, Hermithean, …
▪ Basic operations: A+B, A-B, AB (AB≠BA).
▪ Square matrices
▪ Determinant: det(A)
▪ Inverse matrix A^-1: AA^-1 = I (I is a unit matrix)
▪ …

Applications

	Linear systems of equations
Eigenvalue problem

Linear systems of equations

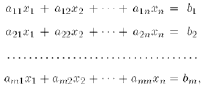
▪ m>n over determined system (data processing)
▪ m=n square case (what we will do)
▪ m<n under determined system

Linear systems in matrix notation

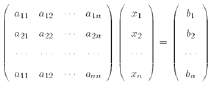
or Ax = b

Two cases for right-hand coefficients

right-hand coefficients b _i ≠ 0
Unique solution if the determinant det(A) ≠ 0

right-hand coefficients b_i = 0
Unique solution if the determinant det(A) = 0

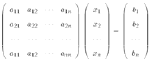
Analytic solutions for n=2

a₁₁x₁ + a₁₂x₂=b₁
a₂₁x₁ + a₂₂x₂=b₂

expressing the first unknown x ₁ from the first equation

x₁ = (b₁ - a₁₂x₂)/a₁₁

and substituting to the second equation we have a
single equation with one unknown x₂.

Gaussian elimination

Since there is no such an operator as elimination
neither in C++ nor Fortran we should translate this
procedure to an appropriate numerical method for
solving systems of linear equations.

Numerical method = Gaussian elimination

Gaussian elimination for n =3

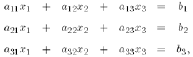
Let subtract the first equation multiplied by the coefficient a₂₁/a₁₁ from the
second one, and multiplied by the coefficient a₃₁/a₁₁ from the third equation.

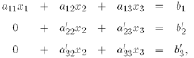
Step 2:
Repeating the same procedure to the last of two equations
gives

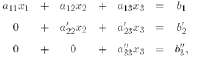
where

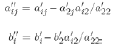
Step 3:

Doing back substitution we will find x₂ and then x₁.

This direct method to find solutions for a system of
linear equations by the successive elimination is
known as Gaussian elimination.

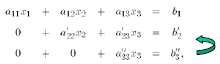
Problems!

zero diagonal elements
round-off errors
ill-conditioned systems
computational time