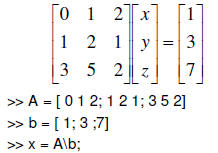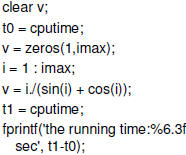MATLAB Primer

MATLAB as a calculator

• Built in functions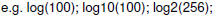

Toolbox: statistics, image processing, signal
processing, Wavelet, control…
>> help
>> help stats
rand(), randperm();

• Built- in Variables
pi, sin(pi/6)

The Real Power of MATLAB

• e.g. solving linear equations in one step

Programming Environment

• Three windows: command window,
workspace and command history

• Three ways to get help:
>> help sqrt
>> lookfor sqrt
>> doc sqrt

All MATLAB variables are matrices

• “MATrix LABoratory”

• A vector is a matrix with one row or one
column

• a scalar is a matrix with one row and one
column

• a character string is a row of column
vector of characters

Assigning Values to Variables

• >> A = [ 3, 2; 3 1; 1 5]

• >> x = [ 5 ;6 ; 7]

• >> y = [ 1 2 3]

• >>A(4,4) = 100 Beyond the existing dimensions
of the matrix?
good or bad compared with other programming
languages?

Using functions to create matrices
and vectors

• linspace
>> u = linspace(0,5,5)
How to create column vectors?

• Create matrices
ones, zeros , eye, diag
A closer look at diag().

Notation

• Subscript notation

• Colon notation
>> s = 1 : 4
>> s = 1 :0.5: 4

• Use colon notation to refer to subsets of
columns and rows
>> A(1:2,1)
>> A(:,1)

String Operations

• String are matrices with character elements.

• String constants are enclosed in single
quotes.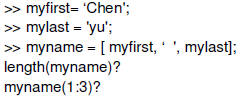

String Functions

• Compare two strings to see if they are
exactly the same
strcmp(‘abc’, ‘abd’);

• Search for a substring with a longer string
findstr(‘abcdef’, ‘def’);
findstr(‘abcdefdfadfadfdef’,’def’);

• help string
strcat(‘chen’,’ yu’);

Built-in Functions

• Scalar function

sin cos tan exp log sqrt floor ceil abs

• Vector functions

max min sum sort median mean

They also work for matrices.

• Matrix functions

eig inv size rank

Working space

• who/whos/clear

• save

• Path

Vectorization

• Use vectorized indexing and logical functions

• Use vector operations instead of loops

e.g. C = A ./3;
A^2 vs. A .^2

• Pre -allocate memory for vectors and matrices

Vectorized Indexing

• x = [ 0.2, 0.55, 0.3,3, 0.7, 1];
index = find(x>0.5)
x(index)

• find(x==1)

• x(find (abs(x-1.5) > 0.5))

Why it is important?
Problem: construct an 50000 entry array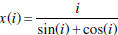

Method 1:

Method 2:	Method 3:

Comparing the times in these three methods