Number and Operations
N&0 – 11 Real Numbers : Real numbers include rational and irrational numbers.
The following diagram shows how the subsets of the real
number system (that have been
defined in this section) are related to each other.
The diagram shows, for instance, that every whole
number is also an integer, a rational
number, and a real number; however, not every integer is a whole number (e.g.,
–3 is an
integer, but not a whole number); not every rational number is an integer (e.g.,
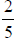 is a
is a
rational number , but not an integer); no irrational number is a rational number;
every
integer is a rational number (e.g., 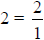 ), and so
on.
), and so
on.
Relationships Between Some of the Subsets of the Real Number System
|
Rational Numbers include whole |
|
|
 |
 |
|
|
|
Irrational Numbers Real numbers that are not rational numbers |
|
|
|
||
Integers {…, –3, –2, –1, 0, 1, 2, 3, …} |
||
|
|
||
Whole Numbers {0, 1, 2, 3, 4, 5, …} |
Every whole number is also an integer, a rational number, and a real number. |
|
N&0 – 12 Ratio: A ratio is a quotient of two
numbers or quantities. Ratios can compare
similar units of measures (e.g., blue cars to red cars), or unlike units of
measures (e.g.,
100 miles per 2 hours). Ratios that compare unlike units are called rates.
The ratio of a to b is typically written as
![]() or a:b. Even though we
write ratios in the
or a:b. Even though we
write ratios in the
form ![]() or a:b to
indicate relative size, numbers in other forms can be interpreted as ratios
or a:b to
indicate relative size, numbers in other forms can be interpreted as ratios
(e.g., 20% represents the ratio 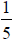 or 1:5 ).
Ratios can express part to whole or part to part
or 1:5 ).
Ratios can express part to whole or part to part
relationships.
Example 12.1 – Ratios:
There are 28 students in a fifth grade class. Ten students have blue eyes.
Fourteen
students have brown eyes. Four students have hazel eyes.
Example of part to whole ratio: The ratio of the students in the class
with hazel eyes to the
students in the whole class is 4:28 or 1:7. The ratio 1:7 means for every one
student with hazel
eyes there are 7 students in the class.
Example of a part to part ratio: The ratio of the students in the class
with blue eyes to the
students in the class with brown eyes is 10:14 or 5:7. The ratio 5:7 means for
every 5 students in
the class with blue eyes there are 7 students in the class with brown eyes.
Example 12.2 – Demonstrates understanding of ratios (part to whole):
Dana and Jamie ran for Student Council President at Midvale Middle School. The
data below represent the voting results for grade 7 and grade 8.
| 7th Grade Votes | 8th Grade Votes | |||
| Jamie | Dana | Jamie | Dana | |
| Boys | 24 | 40 | 25 | 42 |
| Girls | 49 | 20 | 19 | 40 |
John says that the ratio of the 7th grade boys
who voted for Jamie to the seventh
grade students who voted for Jamie is about 1:2. Mary disagrees. She says it is
about 1:3. Who is correct? Explain your answer.
Answer: Mary is correct. John provided the ratio of boys
to girls who voted for Jamie (24 boys:49 girls is
about 25:50 or 1:2). Mary provided the ratio of boys who voted for Jamie to all
the seventh grade students
who voted for Jamie (24 boys:73 seventh grade students is about 25:75 or 1:3).
Example 12.3 – Demonstrates understanding of ratios (part to part):
The graph below shows the number of 6th grade
students at Franklin School and their
favorite pizza toppings (each student voted for only one topping).
Franklin School 6th Graders
Favorite Pizza
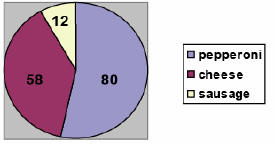
Which statement about the 6th grade students at Franklin School is true?
A) The ratio of students who prefer sausage pizza to the
students who prefer cheese
pizza is about 1:3.
B) The ratio of students who prefer sausage pizza to the students who prefer
pepperoni pizza is about 1:5.
C) The ratio of students who prefer cheese pizza to the students who prefer
pepperoni pizza is about 1:2.
D) The ratio of students who prefer cheese pizza to the students who prefer
sausage
pizza is about 5:1.
Answer: D; The ratio 58:12 is the same as 29:6, which is about 5:1.
N&0 – 13 Expanded notation : In expanded notation a
number is represented by the
sum of the values of each digit in the number.
Example 13.1:
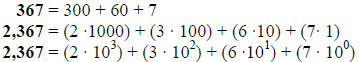 |
(Grades 1 – 3) |
| (Grades 4 – 5) | |
| (Grade 6 – 8) |
N&0 – 14 Equivalent numbers: Two numbers are
equivalent if they share the same
position on a number line 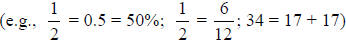 .
.
Example 14.1: 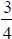 and 0.75 are located at the same place on the number line.
and 0.75 are located at the same place on the number line.
Therefore, they are equivalent.
N&0 – 15 Composition of numbers: Demonstrating
understanding of whole
numbers using composition means that a whole number can be composed by adding
two
or more numbers (e.g., 3 + 5 = 8; 6 + 2 = 8; 2 + 2 + 4 = 8).
N&0 – 16 Decomposition of numbers: Demonstrating
understanding of whole
numbers using decomposition means that a whole number can be decomposed into
multiple addends (e.g., 8 = 3 + 5; 8 = 6 + 2; 8 = 2 + 2 + 4).
Area, Set, and Linear Models
N&0 – 17 through N&O – 19 focus on the
specifications in the GLEs for area, set, and
linear models . Examples 17.1 through 19.2 represent the intent of the
specifications for
area, set, and linear models. In spirit, students should have experience with a
variety of
models (area, set, and linear), and with a variety of relationships (e.g.,
multiple or factor
of the denominator of a fraction ) between the number of parts in the model and
the
fraction, decimal, or percent being represented. In addition, for the most part,
each of
these examples can be slightly changed to focus on fractions, decimals, or
percents. For
example, Example 18.2 might be rewritten to “Circle 50% of the butterflies.”
Also, “part
to whole” is used loosely in the GLEs to mean “part to whole”, “whole to part”,
and
“part to part” relationships.
N&0 – 17 Area model to represent part to whole
relationships: An area
model can be used to represent part to whole relationships for fractions,
decimals, and
percents. The entire model may represents the whole, where the model is divided
into
parts of equal area (e.g., Example 17.3), the model given may represent a part
where the
whole is to be determined (e.g., If 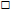 represents 3/4, draw a model that represents 1), or
represents 3/4, draw a model that represents 1), or
the model given may represent a part where another part is to be determined
(e.g., If 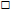
represents 3/4, draw a model that represents 2/3). Examples 17.1 – 19.2 focus on
clarifying the relationship between the number of parts in the model and the
fraction,
decimal, or percent being represented.
Example 17.1: What fraction of the circle is shaded gray?
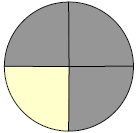 |
 |
In this example, shaded gray. Therefore, the number of parts in the whole, 4, is equal to the denominator. |
Example 17.2: What fraction of the figure is shaded?
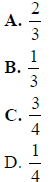 |
 |
In this example,
answer and the number of parts in the whole, 36, is a multiple of the denominator, 4. |
Example 17.3: Shade
![]() of the figure below.
of the figure below.
 |
In
this example, the number of parts in the whole, 2, is a factor of the denominator, 4. |
Answer: These are two ways that students could shade
![]() of the figure.
Students may also shade
of the figure.
Students may also shade
![]() of the figure using
other strategies.
of the figure using
other strategies.
Example 17.4: Shade 75% of the grid.
 |
In
this example, the number of parts in the whole (the grid), 200, is a multiple of 100. |
Answer: Any 150 small squares ( ) in the grid should be
shaded.
) in the grid should be
shaded.
| Prev | Next |