Precalculus I Lecture Notes

2.1 Functions

Relation vs. Function
Value of a function
Implicit form of a function
Domain of a function

Find the domain:

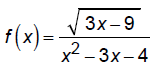
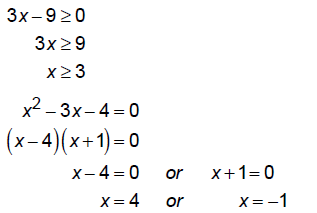
Combing these restrictions we get

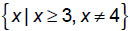
Sums, differences , products, and quotients of functions

2.2 Relations

Identify the graph of a function
Obtain information from the graph of a function

2.3 Properties of Functions

Determine even and odd functions from a graph

Even functions are symmetric about the x-axis (like )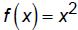
Odd functions are symmetric about the origin (like

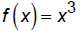
Identify even and odd functions from the equation

For even functions, f(x) = f(-x) for example,

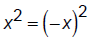
For odd functions, f(x) = -f(-x) for example

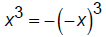
Is 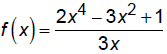even, odd, or neither?

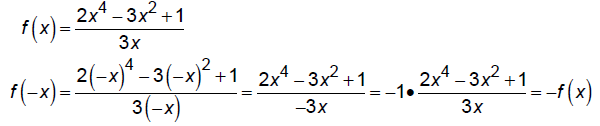
So, the function is odd.

Use a graph to determine where a function is increasing, decreasing, or constant
Local maxima and local minima
Average rate of change of a function

Find Average Rate of Change of from –2 to 1:

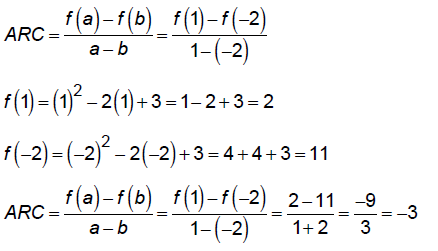
Secant line

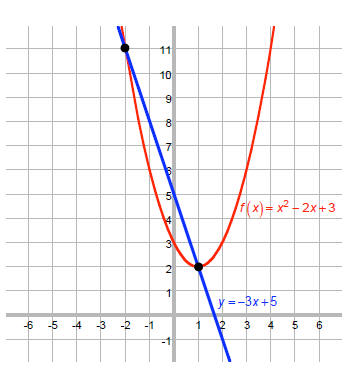
Find equation of secant line for
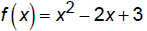
that connects the points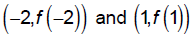
The slope of the line is m = –3, as we calculated above .
The equation of the line is the line whose slope is –3 and
which passes through the points (–2, 11) and (1, 2).

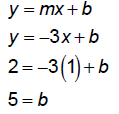
So, the equation is y = -3x + 5

2.4 Library of Functions & Piecewise-defined Functions

Square root , cube root, absolute value, square, cube, reciprocal, greatest integer
Piecewise-defined functions

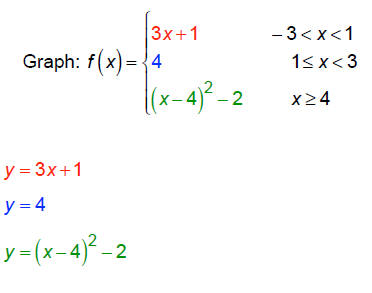
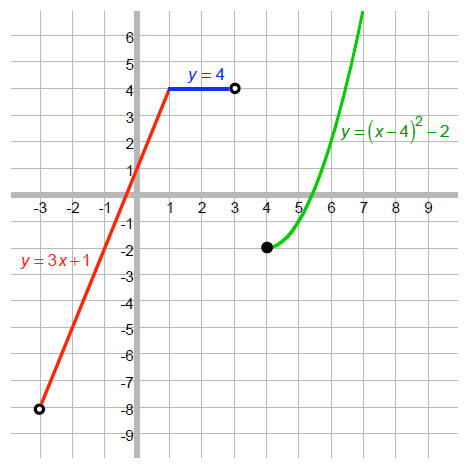
2.5 Graphing Techniques & Transformations

Vertical shifts
Horizontal shifts
Compressions
Stretches
Reflections about xaxis
and yaxis

Graph using transformations:

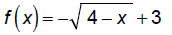
Start with

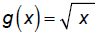
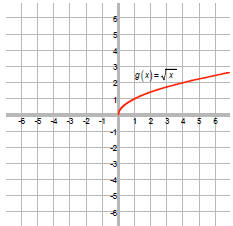
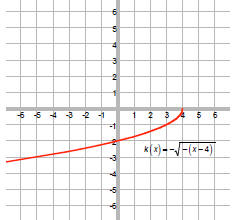
The negative outside the function ( square root )
reflects the graph about the x-axis:

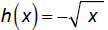
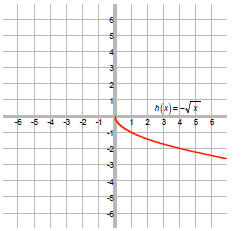
The negative inside the function (square root) reflects the
graph about the y-axis:

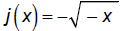
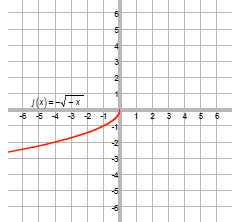
The 4 shifts the graph four units. Since the 4 and x have
opposite signs, the shift is to the right. That is, we can
write this as

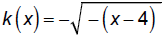
Note that when x = 4, y = 0 so we know it shifts right.

The 3 shifts the graph up 3 units:

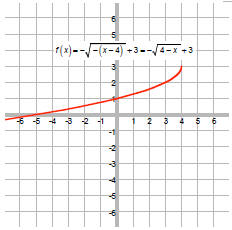
Plot some points
x-intercept:

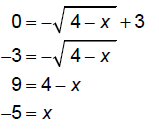
y-intercept:

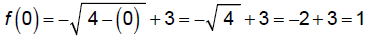
start of graph:

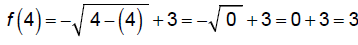
2.6 Mathematical Models & Building Functions

Applications of building and analyzing functions

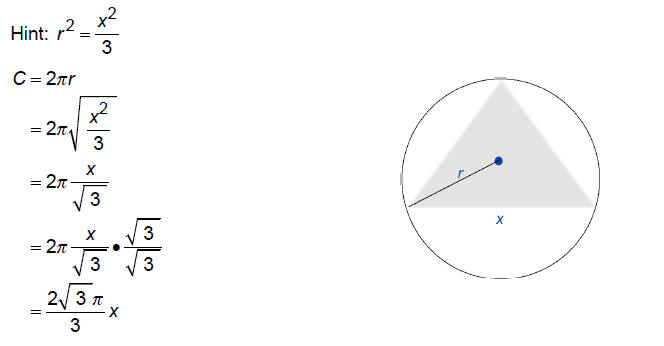
pg 108, #16: An equilateral triangle is inscribed in a circle of radius r. Express the circumference C of
the circle as a function of the length x of the side of the triangle.

3.1 Linear Functions and Their Properties

Graph linear functions
Average rate of change
Determine whether a linear function is increasing, decreasing, or constant
Applications of linear functions (word probs)

Write an expression for the cost C of producing x bicycles in a day if C is a linear function of x, each
bicycle costs $50 to produce, and the fixed costs for the factory are $1200 per day.
The rate or slope is 50 bicycles per day and the y-intercept is $1200 per day.

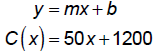
3.3 Quadratic Functions and Their Properties

Define quadratic function
Graph a quadratic function using transformations
Vertex , axis of symmetry, and intercepts of a quadratic function

The x- coordinate of the vertex is

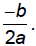
Maximum or minimum value of a quadratic function

3.4 Quadratic Models & Building Quadratic Functions

Applications of quadratic functions (word probs)

A cylindrical silo is made with a circular top and sides using 2000 square feet of metal. Express the
volume V of the silo as a function of the radius r.

The volume of a cylinder is 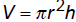. So, we have to express the height in terms of r .

The surface area of the silo is:

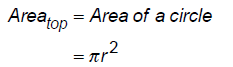
(if you unwrap the silo you get a rectangle of height h and width 2πr , the
circumference of the silo).

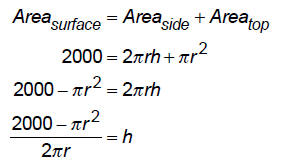
So, we have

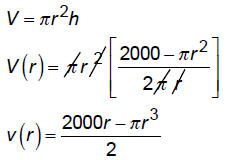
3.5 Inequalities Involving Quadratic Functions

Solve inequalities involving a quadratic function
We will do these when we do rational inequalities on Wednesday.