Inequalities

Chapter 3.3--Inequalities

Inequalities are like equations except that in the place of = we use <,>, ≤, or ≥ .
Treat inequalities exactly as you treat equations , with one important exception. If you multiply the inequality by a negative number, then you must reverse the inequality.

Part 1 Graphing inequalities .
The graph will be done on the board.

Question 3 Graph

x≤0

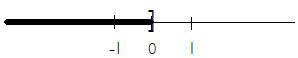
Question 4 Graph

x < 4

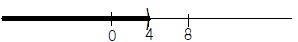
Question 12 Solve and Graph

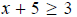
Subtract 5 from both sides

x≥−2

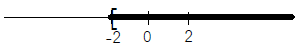
Part 2 Solving inequalities

Question 18: Solve

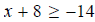
Subtract 8 from both sides x≥−22

Question 42: Solve
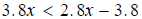
Subtract 2.8x from both sides x < −3.8

If you want to be really proper you can write the solution as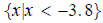

Question 59: Solve −8x ≤ −40

Divide both sides by −8 : [Remember that since we are multiplying/dividing by a negative number that we must reverse the inequality.] x≥5

Question 93: Solve 0.07x < −0.378
Divide by 0.07

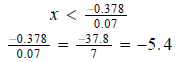
So the solution is x < −5.4

Question 124: Solve:
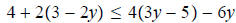
First we simplify by removing parentheses on both sides.

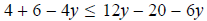
Collect ( Combine ) like terms on each side
10−4y≤6y−20

Subtract 6y from both sides: 10−10y≤−20

Subtract 10 from both sides: −10y≤−30

Divide both sides by −10 . Reverse the inequality.

 y≥3

Question 134: Use the roster method to list the set of positive integers that are solutions of the inequality 13−8a≥2−6a

First we solve the inequality :

Add 8a to both sides: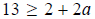

Subtract 2. 11≥2a

Divide by 2 .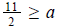

Roster method gives us 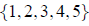because 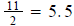, we can’t go any higher than 5.