Quadratic Functions
Graphs
■ Quadratic function (completed square form, contains more info than the
other form)
y = a(x − h)2 + k, a ≠ 0
1. Vertex: (h,k)
Example 1
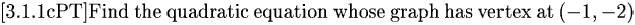
Example 2
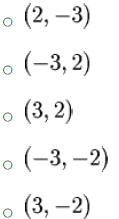
2. Axis of Symmetry is the vertical line through the vertex: x=h
3. The parabola opens …
a) Up if a>0 ( vertex is the minimum point)
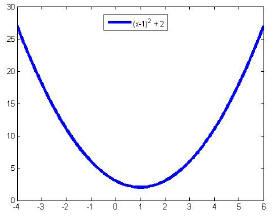
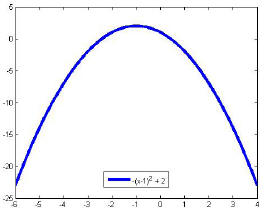
b) Down if a<0 ( vertex is the maximum point)
REMARK: To graph a quadratic function , DO 1-3 (and 4 if necessary)
Exercise 3
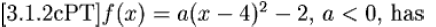
4. Intercepts :
a) y-intercept: set x=0 and solve for y (only one).
b) x-intercept: The number of x -intercepts may be determined by considering the
vertex and the direction the parabola opens. To find the value of x -intercepts,
set
y=0 and solve for x .
■ Quadratic function ( polynomial form )
y = ax2 + bx + c, a ≠ 0
1. Vertex:
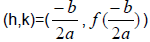
Exercise 4
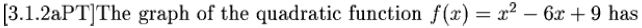
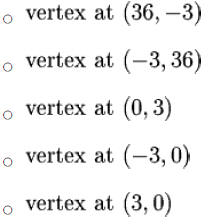
2. Axis of Symmetry: the same as completed squared form ,
i.e.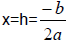
3. Open direction: the same as before
REMARK: To graph a quadratic function, DO 1-3 (and 4 if necessary)
Example 5
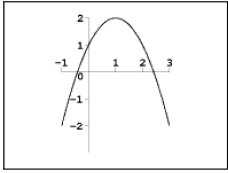
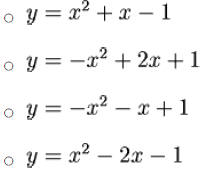
Exercise 6
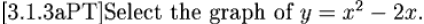
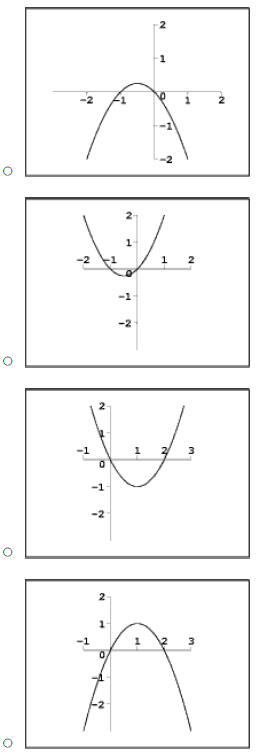
Exercise 7
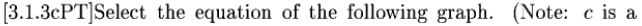
4. Intercepts
a) y-intercept: the same as before
b) x-intercept: by finding out h and k, we can easily rewrite the polynomial
form into
the completed square form .
Exercise 8
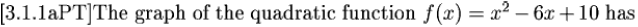
c) x-intercept: or by finding out the discriminant, Δ=b2 − 4ac
Δ=b2 − 4ac >0: TWO x-intercepts (CROSSES)
Δ=b2 − 4ac =0: ONE x-intercept (TOUCHES BUT DO NOT CROSS. Which point on the
x-axis does the graph touch?)
Δ=b2 − 4ac <0: NO x-intercept (DOES NOT TOUCH NOR CROSS)
Exercise 9
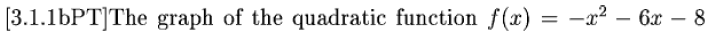
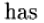
Things You Should Know
You can find out the vertex of a quadratic function by using the formula given
in class, i.e.
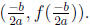Or by completing the square. Completing the square
is equivalent to finding the vertex using the formula. HOWEVER, in most cases,
completing the square can save you much more time. Here, we show some most
common forms , for which you can complete the square swiftly. If none of the
common
forms fits the expression you see , use the formula instead.
f(x) = x2 + 2x + 1 = (x + 1)2, (h = −1, k = 0)
f(x) = x2 − 2x + 1 = (x − 1)2, (h = 1, k = 0)
More:
f(x) = x2 ± 4x + 4 = (x ± 2)2, (h =
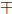2, k = 0)
f(x) = x2 ± 6x + 9 = (x ± 3)2, (h =
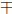3, k = 0)
f(x) = x2 ± 8x + 16 = (x ± 4)2, (h =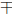
4, k = 0)
Variants:
f(x) = x2 + 8x + 15 = x2 + 8x + 16 − 1 = (x + 4)2 − 1, (h = −4, k = −1)
f(x) = −x2+6x+15 = −(x2−6x)+15 = −(x2−6x+9)+15+9 = −(x−3)2+24, (h = 3, k = 24)
Extra Credit: (Hint: look at the last example to figure out how to deal with the
leading coefficient a if it is not 1)
(1) f(x) = 2x2 + 4x + 9
(2) f(x) = −x2 + 4x − 5
(3) f(x) = −2x2 + 12x + 10
| Prev | Next |