REVIEW OF FUNDAMENTALS
R.4 Straight Lines
PREREQUISITES
1. There are no prerequisites for this section other than some high school
analytic geometry; however, if the material presented in this section
is new to you, it would be a good idea to enroll in a precalculus course.
This section is intended to be a review.
GOALS
1. Be able to find the distance between two points .
2. Be able to write and manipulate equations of the line in its various
forms.
3. Be able to write the equation for perpendicular lines.
STUDY HINTS
1. Distance formula . Don't be concerned about which point is (x1,y1)
and which is (x2,y2) . The squaring process eliminates the need to
make such a distinction. Remembering that the formula is derived
from the Pythagorean theorem makes it easier to recall.
2. Slope formula . As with the distance formula, don't be concerned
about which point is (x1 ,y1) and which is (x2, y2) . The sign will
correct itself when the division is performed .
3. Point-slope form. Replacing (x2,y2) by (x,y) gives the slope as
m = (y - y1)/(x - x1) . Rearrangement yields y = y1 + m(x - x1).
4. Slope- intercept form . Choosing (x1,y1) = (0,b) in the point-slope
form of the line yields y = mx + b .
5. Point-point form. Substituting m = (y2 - y1)/(x2 - x1) yields
y = y1 + [(y2 - y1)/(x2 - x1)](x - x1).
6. Perpendicular lines. Many instructors try to write
harder exam
problems by asking for equations of lines perpendicular to a given
line, so you will benefit by remembering that slopes of perpendicular
lines are negative reciprocals of each other , i.e., if a line has
slope m , then the perpendicular line has slope -l/m .
SOLUTIONS TO EVERY OTHER ODD EXERCISE
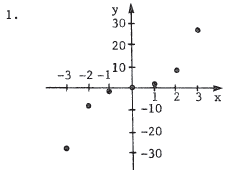 |
For each point (x,y) , go x units along the x-axis and the go y units along the y-axis. |
5. The distance from p1 to p2 is
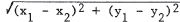 . In
. In
this case, the distance is  .
.
9. The distance from P1, to p2 is
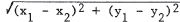 . In
. In
this case, the distance is 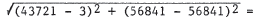
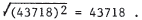
13. The distance from p1 to p2 is
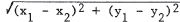 . In
. In
this case, the distance is 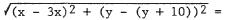
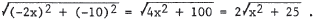
17. The slope of a line through (x1,y1) and (x2,y2) is
m = (y2 - y1)/(x2 - x1) . In this case, m = (6 - 3)/(2 - 1) = 3 .
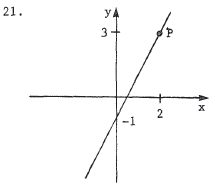 |
The equation of the line with slope m passing through (x1,y1) is y = y1 + m(x - x1) . In this case, y = 3 + 2 ( x - 2 ) = 2 x - 1 . |
25. The equation of the l i n e through (x1,y1) and (x2,
y2) is
y = y1 + [ ( y2 - y1)/(x2 - x1)](x - x1) . In t his case, y = 7 +
[ (4 - 7)/(-1 - 5 ) ] ( x - 5) = 7 + (1/2)(x - 5) = x/2 + 9/2 or
2y = x + 9 .
29. We want t o write the line in the form y = mx + b . Then m is
the
slope and b is the y - intercept . x + 2y + 4 = 0 is the same a s
2y = -x - 4 or y = -x/2 - 2 . Thus, the slope is -1/2 and the
y - intercept is -2 .
33. Write the line in the form y = mx + b . Then m is the slope and
b is they - intercept . 13 - 4x = 7(x + y) = 7x + 7y is equivalent
t o 13 - 11 x = 7y or y = -(11/7)x + 13/7 . Thus, the slope is
-11/7 and the y - intercept is 13/7 .
37. (a) 4x + 5y - 9 = 0 implies 5y = -4x + 9 , i . e . , y = -(4/5)x + 9/5 .
This is i n the form y = mx + b , so the slope is -4/5 .
(b) A perpendicular line has slope 5/4 . When this line passes
through ( 1 , 1) , its equation is y = 1 + (5/4)(x - 1) = (5x - 1)/4
or 4y = 5x - 1 .
41. Using the point-point form of the line , we get the equation
y = 2 + [ ( 4 - 2 ) / ( 2 - 4 ) ] ( x - 4) = 2 + ( - 1 ) ( x - 4) = -X + 6 .
SECTION QUIZ
1. Sketch the line 3x + 2y = 1 .
2. What is the slope of the line 5x - 8y = 4 ?
3. Find the equation of line passing through (3,1/2) and perpendicular
to the line going through (98,3) and (98,-10) .
4. One of your psychotic math friends has seen a little green space ship
and a little red one land in her sink. According to her estimation,
the green ship landed at (-3,l) and the red one landed at (2,4) .
She sees the aliens attacking each other with toothbrushes. The
sink is divided by the perpendicular passing through the midpoint
between the spacecrafts. What is the equation of the line? What is
the distance between the two ships ?
ANSWERS TO SECTION QUIZ
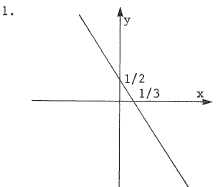
2. 5/8
3. y = 1/2
4. Line: 3y + 5x + 5 ; distance: 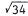 .
.
| Prev | Next |