Why Use a Function Approach when Teaching Algebra?
Example 3
Exploration  Class _____________ Name
_____________
Class _____________ Name
_____________
For each of the following functions, find the maximum or minimum, and
specify the range.

7. Given the absolute value function of the form d|x + e| + f, where d, e, and f
are real numbers and d ≠ 0, answer the following questions:
a. What is the maximum or minimum value of the function?________
b. What is the first (or last) number in the range of the function?________
c. What number, d, e, or f, helps you decide if there is a maximum or a
minimum?______
Example 4 is a guided-discovery exercise that is embedded within other practice homework exercises. A graphing calculator is used on homework exercises too!
Example 4
Find the zero for each function in Exercises 15 - 17. Secondly, find the domain
of each function.
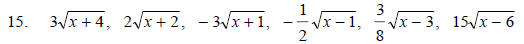
This exercise combines practice as well as discovery and pattern recognition. By the end of the exercise, you have to figure that most students are able to find the zero and domain of the last few functions without the aid of a graphing calculator. We appeal to the brain function of processing abstract mathematics through the visual system . We associate the zeros with the x-axis and functions behaviors.
The enriched teaching/learning environment consists of the pencil and paper group activity , individual homework, a graphing calculator, a TI StudyCard™ stack (not shown), and lecture. We most certainly capitalize on the mind’s ability to recognize patterns. At the same time, the proper use of technology attracts, and keeps, the attention of students.
Teaching Algebra
When finished with the implementation module, you can use functions,
function representations, and function behaviors in the teaching of more
traditional topics. Below are examples requiring the graphing calculator.
Example 5
Teaching Factoring through Activities
Exploration 1 Class
________Name ________________
Class
________Name ________________
1. What is the zero of the function f(x) = 2(x - 3)
2. What is the zero of the function g(x) = 2x − 6?
3. How are functions f and g related ?
4. What is the zero of the function f(x) =−4(x - 3)?
5. What is the zero of the function g(x) = -4x + 12?
6. How are functions f and g related ?
7. What are the zeros of the function f(x) = (x + 1)(x −3) ?
8. What are the zeros of the function g(x) =x2 −2x - 3?
9. How are functions f and g related ?
10. What are the zeros of the function f(x) = (x - 2)(x + 2) ?
11. What are the zeros of the function g(x) =x2 −4?
12. How are functions f and g related?
13. If the zeros of f(x) are –1 and 3, create one possible f(x).
14. If the zeros of f(x) are –4 and –2, create one possible f(x).
15. If the zero of f(x) is 5, create one possible f(x).
16. If the zeros of f(x) are –4, 2, and 1, create one possible f(x).
17. If d and e are the integer zeros of a quadratic function f(x),
create
one possible f(x).
Exploration 2  Class
___________Name _____________
Class
___________Name _____________
1. What are the zeros of the function f(x) = (2x - 1)(x + 3)?
Express them as reduced fractions .
2. What are the zeros of the function g(x) =x2 + 5x - 3 ?
Express them as reduced fractions .
3. How are functions f and g related?
4. What are the zeros of the function f(x) = (3x - 1)(2x + 5)?
Express them as reduced fractions.
5. What are the zeros of the function g(x) =6x2 + 13x - 5
Express them as reduced fractions.
6. How are functions f and g related?
7. What are the zeros of the function f(x) = (2x - 3)(x + 2)?
Express them as reduced fractions.
8. What are the zeros of the function g(x) =2x2 + x - 6?
Express them as reduced fractions.
9. How are functions f and g related?
10. What are the zeros of the function f(x) = (3x - 2)(2x + 3)?
Express them as reduced fractions.
11. What are the zeros of the function g(x) =6x2 + 5x - 6?
Express them as reduced fractions.
12. How are functions f and g related?
13. If ½ and 3 are the zeros of a quadratic function f(x),
create one
possible f(x) containing integer parameters.
14. If 2/3 and −3 are the zeros of a quadratic function f(x),
create one
possible f(x) containing integer parameters.
15. If 2/3 and −1/4 are the zeros of a quadratic function f(x),
create one
possible f(x) containing integer parameters.
16. If a/b and d/e are the zeros of a quadratic function f(x),
create one
possible f(x) containing integer parameters.
17. Describe in your own words any connection you see between the zeros of a
function and the symbolic form of the function.
Exploration 3 Class
____________Name _____________
Class
____________Name _____________
In the first two explorations, you learned about the connection between function
parameters and the related zeros of the function. Below is a quick review and
then a continuation of the exploration.
1. Find the zeros of the function y = (2x + 1)(x − 3).
2. Find the zeros of the function y = 2x2 − 5x − 3.
3. Why are the zeros the same for y = (2x + 1)(x − 3) and y = 2x2 − 5x − 3?
4. Find any polynomial whose zeros are -5 and 5.
5. Find any polynomial with integer parameters whose
zeros are -4/5 and3.
6. Based on what you learned in the first two explorations,
write the function y = x2 + x − 2 another way using
the zero-parameter connection.
7. Based on what you learned in the first two explorations,
write the function y = x2 − 4 another way using the
zero-parameter connection.
8. The function y = 2x2 − 5x − 3 can be symbolized
another way. Write it using other symbols with integer parameters.
9. Why do you think the function y = x2 + 4 cannot be
written in different symbolic form with integer parameters?
10. Why do you think the function y = x2 + 2x + 4 cannot be
written in different symbolic form with integer parameters?
11. When you re-write a function like y = x2 + 3x − 28 as y = (x + 7)(x − 4), we
say you are re-writing in factored form. Or we say you are factoring. For each
of the following functions, re-write them in factored form. That is, factor
them.
a. 3x2 − x − 2
b. x2 − 9
c. 20x2 + 33x − 36
More on Teaching Algebra: Teaching the Less Than Property
A traditional option (when not using a function approach) is to state the
property and then use it in several examples.
If |x| ≤ a for some positive number a, then -a ≤ x ≤ a.
But the problem is; what is it associated with, other than absolute values? What are the associative cues for recalling this property? We cannot count on practice for long- term memory retention nor understanding. Where is the connection with number sense? That is, how have we capitalized on the brain’s primary number sense, and learned number sense from grade school? What is the enriched environment in the teaching process? How did we help the brain use its visual processing abilities of the abstract mathematics? What was used to procure the attention of the student?
Thinking from a function approach, we know that students have seen all representations of absolute value functions from the implementation module. Given y = d|x + e| + f, they know what behaviors the d, e, and f parameters control. They have traced on the graph to make connections between representations and involved their learned number sense. They have associated absolute values with various real-world contexts. Students have made parameter-behavior associations with the more common function y = d(x + e)2 + f. Technology and the various contexts used in the original work with absolute value data relationships have gotten their attention.
Example 6
Teaching the “Less Than Property” for Absolute Values, A Classroom Activity
In teaching from a function approach we start with the graph of the function y =
|x|
and the graph of a constant function y = some positive number, for example y =
2. See Figure 10.
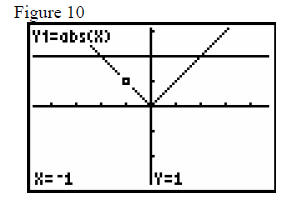
What do we discover about |x| as we trace back and forth between x = −2 and x = 2? It is that it is always less than or equal to the positive number 2. Is this pattern true for the positive number 3 or 1.7 or 19?
Hmmm, it seems that if |x| ≤ a then −a ≤ x ≤ a. Do we also learn something about x when |x| > a? Now is the time for formalizing the property with abstract symbols, followed by “thinking required” practice.
Observation
When teaching algebra from a function approach, yes, I grab the graphing
calculator first. Used in teaching algebra from a function approach, the
calculator facilitates the kind of teaching that facilitates student
understanding, and long-term memory of algebra.
Seven Reasons for Using a Function Approach
Here are some issues to consider when making decisions about teaching algebra
using a function approach versus the traditional equation-solving approach.
The research shows that:
• We remember algebra longer and have better memory by using associations – made
through function permeating the content. That is, students are more likely to
remember the mathematics taught because we capitalize on associations made
through using a function approach.
• Learning is made simpler , faster, and more understandable by using pattern
building as a teaching tool. In a function approach, almost all of the pencil
and paper activities, e-teaching activities, and class discussions use pattern
building to reach a generalization about a concept or skill.
• Students cannot learn if they are not paying attention. The graphing
calculator is used to draw attention to the mathematics through its basic
functionalities including, various application software.
• Without visualizations, students do not understand or remember the mathematics
as well. In the function approach visualizations are used first before any
symbolic development. This greatly increases the likelihood that students will
remember the mathematical concept being taught.
• Considerable brain processing takes place in the subconscious side of the
brain, including a learning module. To make this processing possible for our
purposes, the brain must be primed. The function implementation module and early
learning activities prime the brain for all the algebra that follows.
• The enriched teaching/learning environment promotes correct memory of
mathematics content. The wide variety of teaching activities facilitated by the
function approach provides the enriched environment.
• Contextual situations (represented as functions) provide meaning to the
algebra learned. Algebra taught without meaning creates memories without meaning
that are quickly forgotten.
| Prev | Next |