Solving Dierential Equations with Long Division
Solving Differential Equations with Long Division
1 Introduction
This is a handout to describe the basics of the long division technique for
solving differential equations. This
technique evolved from my discussions with 18.03 students over the course of the
year. While it won't solve
every 18.03 problem, it will solve a good many.
For those of you who are familiar with 18.03, this technique can be considered a
replacement for the
undertermined coefficients technique in its capacities.
2 Background
2.1 What we need to know from calculus
In calculus, we learned about the derivative. Here is a short list of important
facts about the derivative:
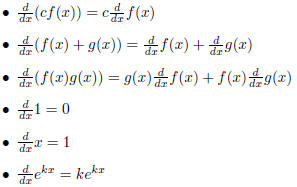
These are all the facts we need to know to use
![]() on any polynomial or
any polynomial times an
on any polynomial or
any polynomial times an
exponential . For example,
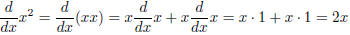
and
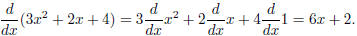
There are other properties of
![]() not mentioned here,
like the chain rule, but we will not need them.
not mentioned here,
like the chain rule, but we will not need them.
2.2 What we need to know about integration
Integration was the first differential equation one solves . It asks, for some
g(x), find a f(x) such that
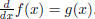 Solving this problem is easy if g(x) is a
polynomial,
Solving this problem is easy if g(x) is a
polynomial,
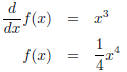
or if g(x) is an exponential,
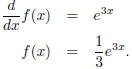
We quickly learned that since 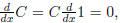 that many different solutions were possible for a given
that many different solutions were possible for a given
integration problem,
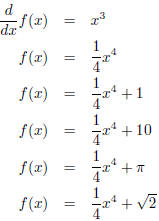
so to capture this idea we wrote 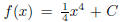 where C was some constant about which we had no
where C was some constant about which we had no
information.
If we describe our differential equations with fractional notation, the
integration problem is
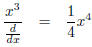
or, more generally,
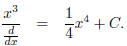
3 Simple differential equations with simple solutions
Complicating the integration problem:
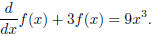
In other words, we are looking for a function which when 3
of it is added to its derivative, the result is 9x3.
In fractional notation, we might write
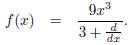
Althought
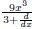 looks a bit alien, by thinking of it as a division, there is a straightforward
way to get an
looks a bit alien, by thinking of it as a division, there is a straightforward
way to get an
answer,
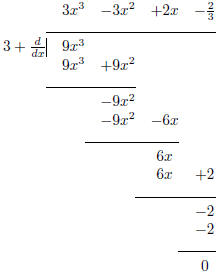
Is
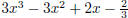 really a function that if you add 3 of it to its derivative you get 9x3?
This is easy
really a function that if you add 3 of it to its derivative you get 9x3?
This is easy
to check,
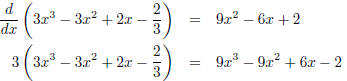
and the long division process has worked.
We can make up harder problems by taking more derivatives or making the right
side more complicated
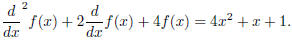
The long division method can still give us a solution of
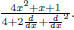
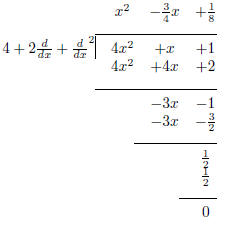
Again, the answer 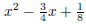 is
not hard to check,
is
not hard to check,
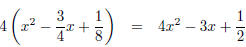
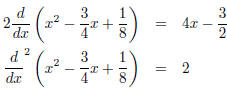
which sums to 4x2 + x + 1 as it should.
3.1 Why does long division work?
Under certain common conditions, the long division technique above gets a
solution. Those conditions are:
•
The numerator is a polynomial in x
• The denominator is a polynomial in
![]()
•
The denominator has a (non- zero ) constant term
Under these conditions, long division will produce a polynomial in x which is a
solution of the differential
equation associated with that fraction.
Put in more mathemtical terms :
Theorem 3.1 (Long Division). The differential equation
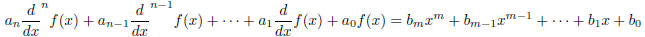
has a solution by the long division method whenever
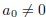 and that solution is a polynomial of degree m or
and that solution is a polynomial of degree m or
less.
Proof. We can see that if m = 0, so the right hand side is b0, then
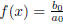 is a solution (all its derivatives
is a solution (all its derivatives
vanish since f(x) is constant). The degree of 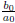 is 0, because it is a constant, so the statement about degrees
is 0, because it is a constant, so the statement about degrees
holds too.
More generally, at each step of the long division method, we approximate our
solution f(x) with 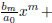
R(x) where R(x) is the rest. Plugging this into the differential equation gives
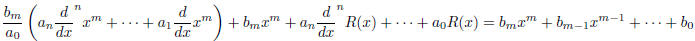
and moving terms from the left to the right (cancelling
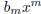 )
)
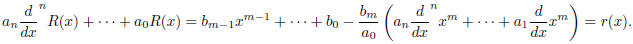
The operations on the left hand side are the same, only in
terms of the new function R(x) and the right
hand side, r(x), is a new polynomial of degree m - 1 or less, corresponding to
the remainder after the one
step of long division. In fractions
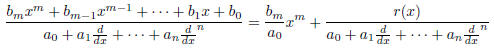
Thus, as we repeat, we reduce the degree of the right hand side with each step, until it is just a constant.
4 Solving harder problems
The long division method itself only let's solve
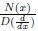 when N(x) is a polynomial in x and
when N(x) is a polynomial in x and
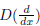 is a
is a
polynomial in 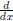 with D(0) ≠ 0. There
are some tricks we can use to extend the method beyond these
with D(0) ≠ 0. There
are some tricks we can use to extend the method beyond these
obstacles.
4.1 The constant part of the denominator vanishes
An example is 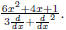 This fraction stands for the
differential equation
This fraction stands for the
differential equation
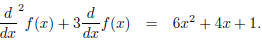
That is the same as making up some intermediate function g(x) and saying
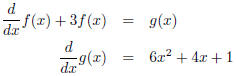
which is solved by
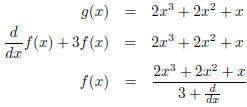
which is a fraction we can solve with long division.
This could just as well be written compactly as
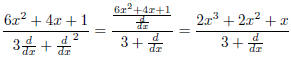
with
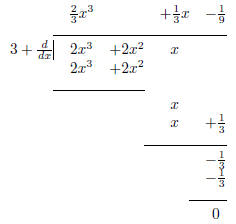
giving a solution.
Put in more mathemtical terms:
Lemma 4.1 (Integration step). A solution to
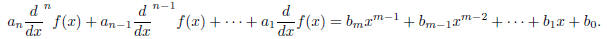
can be found by taking any solution of
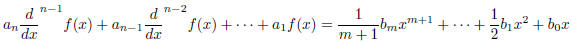
4.2 More complicated numerators: exponentials
The product rule tells us that
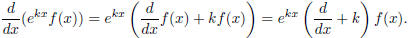
This is true for higher derivatives as well,
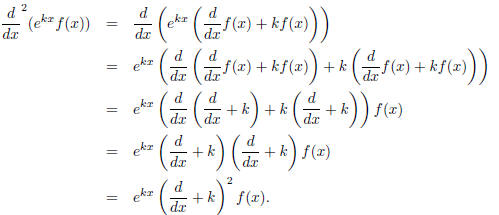
Every time 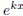 moves left
past a
moves left
past a ![]() it turns that
it turns that
![]() into
into
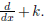 This fact is called the exponential shift
law .
This fact is called the exponential shift
law .
We can use this to do fractions with exponentials in the numerator ,
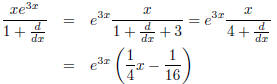
where we used long division for
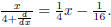 We can check,
We can check,
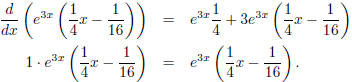
Lemma 4.2 (Exponential shift step). A solution to
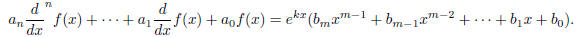
can be found by taking any solution of
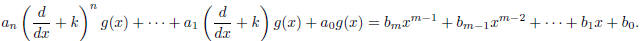
and setting 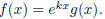
| Prev | Next |