The Integers and Rational Numbers
Proposition 1.2.4. Suppose a = a'f and b = b'f, in which case we say that
f
is a common factor of both a and b. Then:
(i.e. we can cancel common factors of the numerator and denominator.)
Proof: We need to show that
. But:
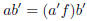
by substituting , and likewise,
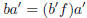
so indeed the two fractions are equivalent.
Multiplication distributes with addition. Proof:
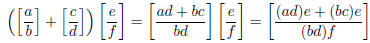and
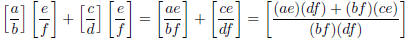
There is a common factor of f in the numerator and denominator of the
second fraction. Once we cancel it (Proposition 1.2.4), we see that the two
rational numbers are the same !
Now for some extra goodies:
The additive identity is the rational number :
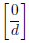
(and it doesn’t matter what d is, as long as it isn’t 0).
Proof: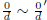 
since 0 × d' = 0 = 0 × d, so
all choices of denominator give
the same rational number (namely the slope of the x-axis!). Next:
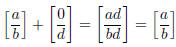
(using Proposition 1.2.4 again) proves that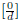 
is the additive identity.
Notation: Mathematicians always denote the additive identity by:
0
so we will, too.
Every rational number has an additive inverse. Proof:
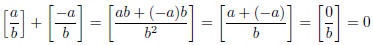
using Proposition 1.2.4. So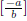 
is an
additive inverse to 
.
As in Proposition 1.2.2, this is the only additive inverse!
Definition of Subtraction:
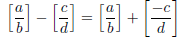
As always, subtraction is addition of the additive inverse
The multiplicative identity is the rational number:
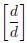
(and it doesn’t matter what d is, as long as it isn’t 0)
Proof: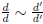 
since dd' = d'd. So it
doesn’t matter what d is, and:
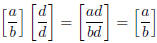
by Proposition 1.2.4. This is what we needed to prove. Again, it is easy to see
that this is the only multiplicative identity.
Notation: Once again, we follow mathematical custom and write:
1
for the multiplicative identity.
Every rational (except 0) has a multiplicative inverse. Proof: Every
rational number other than 0 is of the form
where a ≠ 0. Then:
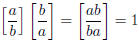
so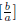 
is the one and only multiplicative
inverse (or reciprocal) of
.
Definition of Division (by anything other than 0):
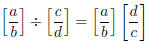
(i.e. division is multiplication by the reciprocal)
Finally, I want to talk about one last definition:
Definition of Lowest Terms : An integer fraction (not rational number!)
is in lowest terms if b > 0 and a and b have no common factors other than 1
and -1 (which are common factors of all integers, hence “uninteresting”!).
Proposition 1.2.5. Every rational number
contains exactly one
fraction
in lowest terms (in the equivalence class).
Idea of Proof: Start with the fraction 
, which may not be in lowest terms.
By cancelling out all the (interesting) common factors of a and b and also −1 if
necessary (to make b > 0) we arrive at a fraction in lowest terms. This shows
that there is at least one fraction in lowest terms in the equivalence
class .
To see that there cannot be more than one, we will need to know a bit more
about prime numbers, which we will work out later in the course (§2.2).
This allows us to redefine one more time:
Q = {integer fractions that are in
lowest terms}
In particular, we get an inclusion of sets:
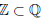
by identifying each integer a with the fraction
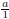, which is clearly in lowest terms.
When we do this, we see something very important. Namely:
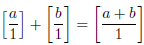and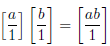 
so addition and multiplication are the same regardless of whether we view a and
b as integers, or as rational numbers!
Finally, as in §1.1, we finish with another gem from ancient Greece:
Theorem (Pythagoras): There is no square root of 2 in Q.
Proof: If there were a rational number square root of 2, then:
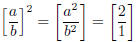
would tell us that:
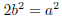
so that 2 divides a2. But then it would follow that 2 divides
a since the square
of an odd number is odd. Thus a = 2c for some c, and then:
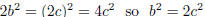
But then 2 divides b2 so it would follow as above that 2 divides b.
In other
words, 2 would be an interesting common factor of a and b. All this would
be true no matter what fraction a/b we chose to represent the rational square
root of 2. In other words, there would be no way to put such a rational
number in lowest terms! This contradicts Proposition 1.2.5, so there cannot
be such a rational number.
Recap: Rational numbers are equivalence classes of
integer fractions, and they
have a very satisfactory arithmetic, with additive inverses and multiplicative
inverses (of everything except 0) allowing us to define subtraction and exact
division (by anything except 0). On the other hand, from the point of view
of geometry, they are less satisfactory, since a perfectly reasonable length (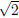
)
cannot be represented by a rational number.
1.2.1 Integer and Rational Number Exercises
In the first three exercises, we consider arithmetic in an abstract setting. The
idea is that many of the results of this section are not special properties of
the integers or rational numbers, but rather follow from the laws of arithmetic
themselves.
2-1 Suppose S is a set and + is an addition rule for elements of S that
satisfies:
• the associative law: (s + t) + u = s + (t + u) for all s, t, u ∈ S, and
• the commutative law: s + t = t + s for all s, t ∈ S.
(a) Prove that there is at most one additive identity element in S. That is,
prove there is at most one element z ∈ S such that:
s + z = s for all s ∈ S
( Mathematicians tell us to rename this element 0)
Hint: If y is another additive identity, think about y + z in two ways.
(b) Assuming that there is an additive identity element (renamed 0), prove
that each s ∈ S has at most one additive inverse in S. That is, prove that there
is at most one element t ∈ so that:
s + t = 0
(Mathematicians tell us to rename this element −s)
(c) Prove that if s has an additive inverse −s, then the additive inverse of
−s is s. That is, prove: −(−s) = s
Definition: A set S with an addition rule + with a 0 and additive
inverses of
everything is an Abelian group .
2-2 If S is an Abelian group with a multiplication rule × satisfying:
• the associative law: (s × t) × u = s × (t × u) and
• the two-sided distributive law with addition:
(s + t) × u = s × u + t × u and u × (s + t) = u × s + u × t
(we will not, for now, assume that multiplication is commutative!)
(a) Prove that s × 0 = 0 and 0 × s = 0 for all s ∈ S.
Hint: Consider s × (0 + 0) and (0 + 0) × s.
(b) Prove that for all s, t ∈ S
s × (−t) = −(s × t) and − (s × t) = (−s) × t
Hint: Consider s × (t + (−t)) and (s + (−s)) × t.
(c) Prove that (−s) × (−t) = s × t for all s, t ∈S.
Definition: An Abelian group S with an associative and two-sided
distributive
multiplication rule is called a ring.
Examples: Z and Q are rings with a commutative multiplication rule. The
n × n matrices (for n > 1) with entries in Z or Q (or any ring) are themselves
a ring with a non-commutative matrix multiplication!
2-3 Suppose S is a ring with a commutative multiplication rule.
(a) Prove that there is at most one multiplicative identity in S.
(Mathematicians tell us to rename this 1)
(b) Prove that each element s ∈ S has at most one multiplicative inverse
(reciprocal) element t∈S.
(Mathematicians tell us to rename this 1/s.)
(c) Prove that 0 does not have a multiplicative inverse (unless 0 = 1). Discuss
what the ring would look like if 0 = 1.
(d) If s has a multiplicative inverse, prove that:
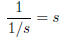
Hint: Exercise 2.3 is very similar to Exercise 2.1.
Definition: A ring S with a commutative multiplication and a
multiplicative
identity 1 ∈S, such that every element of S (except 0) has a multiplicative
inverse is called a field.
Our Only Example of a Field (so far): Q is a field.
2-4 Prove the following:
(a) If a, b∈ Z and ab = 0, then either a = 0 or b = 0 (or both).
Hint: If a and b are both natural numbers, then ab ≠ 0 because it is a natural
number! What are the other possibilities for a and b?
(b) If a, b, c ∈ Z and ab = cb and b ≠ 0, then a = c.
Hint: Find a way to use (a).
2-5 Recall that:
exactly when
ba' = ba'
We’ll check “ algebraically ” that this really is an equivalence relation.
(i) Reflexive. This is the commutative law for multiplication!
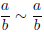because ba = ab
(ii) Symmetric. This is also the commutative law for multiplication.
If then ba' =
ab' but then b'a = a'b so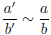
(iii) Transitive. This is your exercise! You need to explain why
ba' = ab' and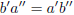 
together imply that
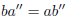
2-6 Consider the two rational numbers:
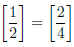and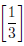 
Explain carefully why the fact that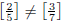 
shows that “dumb” addition:
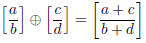
is not well-defined on rational numbers.
2-7 Prove Pascal’s identity. For natural numbers m < n,
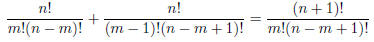
Remark (for your enjoyment): This proves that the “binomial coefficient:”
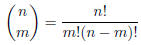
is the m + 1st number in the n + 1st row of Pascal’s Triangle:
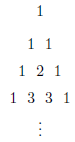
2-8 The ancient Egyptians had some ideas about
fractions, though they apparently
didn’t like to subtract, didn’t like numerators, and didn’t like repetitions.
The “Egyptian fraction” expansion of a rational number between 0 and 1 is a
sum of distinct fractions, all of the form:
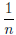
Here are some examples (I’m going to drop the cumbersome brackets around
rational numbers in this problem and from now on!):
(
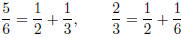
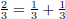is not an Egyptian fraction expansion
because the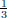 
repeats)
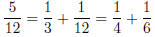
(so sometimes there is more than one possible expansion).
(a) Find Egyptian fraction expansions for the numbers:
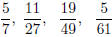
(b) Devise a strategy for finding an Egyptian fraction for any m/n (assuming
that m < n). Hint: You might find induction useful. Apply your strategy to
the four numbers above (your calculator will not give you enough accuracy for
the last two...you will need a computer!).
| Prev | Next |