The Teaching of Fractions and its Discontents

Despite my background as a research mathematician, I have actually had quite a bit
of experience writing mathematics at or near the middle school level, and a substantial
amount of that e ort was concerned with the teaching of fractions in the higher elementary
grades. It is an issue I take seriously because I am concerned with what it takes
in K-12 math education to produce students who are "math-ready" for the demands of
college level work. At some point, more than 50% of high school graduates will enter a
college level program, many of which have Calculus-level math requirements. No one can
tell in advance who will or will not seek such career paths, so college-readiness should be
the ultimate goal of any sound K-8 math program.

The topic of fractions is a major stumbling block for many students, otherwise we
would not be here tonight. Nevertheless, it is crucial that students become adept at
handling fractions - and by that I mean fractions as fractions, and not numbers punched
into a calculator - because fractions and their arithmetical properties provide the bedrock
of intuition upon which all later concepts of algebra and Calculus rest.

What I will say is partly inspired by my reading of portions of a forthcoming book
directed toward the concerns of K-12 teachers by Prof. Hung-Hsi Wu, of Berkeley,
the recent book Elementary Mathematics for Teachers by Thomas Parker and Scott
Baldridge, and from my own experience working with Stanley Ocken of CCNY creating
a mathematically coherent account of how fractions work (unpublished), used to train
tutors providing remedial math assistance to 9th graders at the University Neighborhood
High School in New York City.

Let me begin with what I see as the preconditions for any program that aspires to
the successful teaching of fractions. Although I may not have time to pass on to the next
topic - specific pedagogical issues I see in the teaching of fractions - I have nevertheless
included a few thoughts on these at the end of the the written article I have prepared
for this convocation. I may have an opportunity to mention them in the open discussion
sessions.

The Suppport Base for Teaching Fractions in Grades 5-8

In my opinion the following issues must be taken into account if we hope to resolve the
difficulties commonly encountered in teaching fractions.

1. Teaching to mastery. Math is different from many other subjects - the sciences,
for example - owing to its intrinsically "vertical" structure. Its concepts build upon each
other, layer-by-layer, as we progress from counting to fractions, to algebra, to calculus,
and beyond. As you go higher you come to realize more and more ways in which the
external world is mirrored in mathematics. But, each level must be mastered so students
can confidently use its concepts as they reach for the next level of sophistication. The
need for mastery before proceding to the next level is not given the respect it demands
in quite a few K-8 math curricula I have reviewed.

The need for step-by-step mastery is evident in microcosm in the teaching of fractions
in the K-8 grades, where the natural progression of concepts is pretty clear to any
mathematician.

2. The need for logical progression and clear definitions. It has often been said
that "You cannot teach what you do not understand." In discussing fractions we are concerned
with its corollary: "You cannot really understand what has never been defined."
I will have more to say about this, but for the moment let me say that mathematics is
founded on clear definitions, and the logical relations between them.

There is a simple and easily understood definition of a fraction as a (rational) number:
a point on the number line whose position can easily be found from the symbol m/n that
represents it. By grade 5 most children understand the concept of number line - it is
visual and intuitive. The trouble begins when one fails to make a clear the distinction
between a fraction (a number) and the symbol that represents it. Students soon discover
that the same number (length of a line segment) can be represented by many symbols,
as with 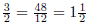, etc, and get confused if there is not one basic definition to fall back
on. It is not so confusing if you think of it this way: the family pet is often referred to
by various whimsical names, but whatever the name-of-the day, it is still the same pet.
Even so with fractions and their representations.

3. Sometimes less actually is more. This seems to be the era of bloated sets of
instructional materials. I have in my office a cubic foot of student booklets for Grade 6
in a well-know math program; the Singapore Math materials for Grade 6 consist of two
slim textbooks and two practice Workbooks [hold them up to view]; the entire set costs
about $45 online at singaporemath .com.

Part of the trouble stems from ill-considered State standards, which desperately need
pruning in the face of "topic inflation," with every Committee member shoehorning in
his or her pet topic, whose coverage then becomes mandatory statewide. There is no
need for this, and it is counterproductive. The most successful countries in the world
- Singapore, China, Japan, etc - have lean and clear-cut curricula which allow them to
make sure that students achieve real mastery of the topics that are covered.

4. The need for clear, concise, mathematically sound textbooks. Teachers,
students, and even parents need an actual textbook, with supporting practice workbooks,
that students can study at home to reinforce what they have learned in class. Without a
coherent textbook, parents cannot help their children learn and are disenfranchised from
the educational process. Without a textbook students cannot refer back to previous
topics relevant to the tasks at hand. On both counts the absence of a coherent textbook
seems to me indefensible.

A good text should strike a balance between explanation of concepts, worked examples,
exploratory projects illuminating the meaning of mathematical concepts, and plenty
of practice problems (perhaps in a separate workbook); contrary to popular belief, it is
not mandatory that practice problems be dull and boring - see the Singapore texts and
Workbooks for example. The text should also adhere to the principles set forth in 3.
The following quote from Wu is relevant here:

A mathematician approaching the subject of fractions in school cannot help
but be struck by the total absence of the characteristic features of mathematics:
precise definitions as a starting point, logical progression from topic to topic,
and most importantly, explanations that accompany each step. This is not to
say that teaching of fractions ... should be rigidly formal from the beginning.
Fractions should be informally introduced as early as second grade (because
even second graders need to worry about drinking "half a glass" of orange
juice ):

5. Teachers must know their subject. To teach fractions effectively, a teacher
needs to know fractions and their applications cold. A good check (borrowed from Herb
Clemens via Prof. Wu): can the instructor explain why 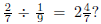I can fully
sympathize with the panic response that often ensues - fractions is a subtle and many
faceted topic, and it often takes a lot of experience to gain command of it. I applaud
e orts to enhance the math content training of K-8 teachers who face these challenges.
But until the millennium arrives, perhaps the time has come for us in the U.S. to consider
the turning math teaching in the upper middle grades to cadres of well-trained and
experiences math specialists, of the sort described in Li-Ping Ma's book on her experiences
in China. This seems to be standard practice in K-8 math (and science) teaching in China,
Japan, and other highly successful countries.

Some Pedagogical Issues in the Teaching of Fractions

I list items as they arise in the natural sequence of fraction concepts.

1. The very definition of "fraction" is a source of difficulties. In his book Wu
lists 5 different commonly used "explanations" of what a fraction "is." Is it any wonder
kids get confused by the concept? In my view there is just one basic definition: a fraction
m/n is a rational number , a point on the number line whose location is easily found once
you are given the symbol m/n using a definite algorithm: divide the unit interval into n
equal pieces, then chain together m of them.

2. A fraction vs the symbols m/n that represent it. The distinction between a
fraction (a number) and the symbols used to represent it is not always made. The symbol
is not "the number"; it is a mnemonic device that encodes the information we need to
locate the number. But the encoding process is a bit redundant, with the result that a
single number can have many different symbolic representations such as
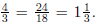
The foundational concept of " equivalent fractions " (which should perhaps be referred to
as "equivalent representations") cannot be understood until students understand that m/n
is just a label for the actual object. They should be shown many examples illustrating
why many different labels can be applied to the same object, until they are comfortable
with the idea.

3. Dealing with the ambiguity in the symbol m/n . This discussion of equivalent
fractions should culminate in a clearly stated algorithm for "building up" and " reducing "
fractions, namely the identity

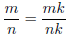for any whole number k

I have seem many rambling discussions and interpretations of equivalent fractions that
never get around to stating any such clear-cut final result, which students can then use
at the next level in their study of fractions.

4. Confusing a fraction with its many real world manifestations. Fraction have
many useful interpretations in real life, and students often confuse the mathematical
concept with its interpretations. The fraction 5/8 is a number, but in specific real-world
situations that number might be regarded as describing: a ratio, a rate, a percentage,
or a collection of pizza slices. There is just one definition of fraction; all other aspects
are interpretations of this mathematical concept in specific real world situations. No
single interpretation can encompass the others; the single basic definition of fraction as
a number subsumes all its applied interpretations. In short,

If you know the one big thing, you can do many little things.

This is the whole point of mathematical abstraction, and the source of its power.

6. The addition algorithm made confusing. The natural way to explain fraction
addition is to first deal with sums involving fractions with the same denominator such as
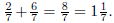For these, addition of fractions interpreted as lengths of line segments is
just like addition of whole numbers. Then one employs the rules for handling equivalent
fractions to get the following algortihm for adding unlike fractions

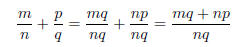
Done!
I have been told by various people that this "cross-multiply" algorithm is not allowed.
(By whom?) To the contrary, what is unnatural is the usual definiton in terms of greatest
common divisor and all that. This concept only comes into play when you go to simplify
the output of this algorithm, and even then is often completely unnecessary if you are
comfortable working with equivalent fractions. The traditional definition, by mashing
together two completely different ideas, needlessly confuses the issue.

7. Distinguishing the (+) operation from the algorithm for computing it.
The (+) operation can be explained geometrically without invoking anything like the
cross- multiply formula . But to get beyond gluing together strips of paper and measuring
their lengths, we need an algorithm - a procedure that tells us how to get from input to
output

Input: The symbols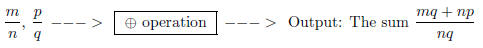

The notion of algorithm should be explained and emphasized here. The creation of
efficient algorithms for finding answers is the soul of mathematics.

There is much more to be said about the next steps in the natural progression of fraction
topics.

•Multiplication of fractions
•Division of fractions; division as the solution of an inverse problem
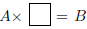
involving fractions A and B
•The algebraic rules that govern the arithmetical operations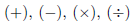on
fractions, and their relation to the algebraic operations on whole numbers.

•The traditional applications of fractions: ratios, rates, percentages, etc. which must
all be explained in detail to give students a proper understanding of the many ways
fractions turn up in day-to-day life.

This brief presentation is not the place for the extensive discussion these topics deserve.
For further reading, I commend Prof. Wu's book to you, expecially the brief Appendix to
Chapter 2 which specifically addresses the common difficulties encountered in teaching
fractions.