Thank you for visiting our site! You landed on this page because you entered a search term similar to this: adding, subtracting, multiplying, dividing integers, here's the result:
How to Add, Subtract, Multiply, and Divide Polynomials
Introduction and Vocabulary
A one variable polynomial, the kind you will most often see, is an algebraic expression made up from adding, subtracting, and multiplying of the variable and numbers. All such things can be written as a sum of products of numbers and powers of the variable, and when you put this in descending order of powers it is called the standard form of the polynomial. Here are some examples of polynomials in standard form.x7-3x+1, x+5, 6x3-7x2+6x-9, 5, x, 2345x17, x5+x4+x3+x2+x+1, 8
The numbers that are multiplied by the powers of the variable are called coefficients. They can be . You can have polynomials with complex number coefficients as well, but most of the ones you will see in algebra classes will have real numbers as coefficients. I only used whole numbers, because they are easier to write down in html. Actually not all of the numbers I used were whole numbers, some of them were negative, because I said 'sum' in the description above, and when you are talking about coefficients you assume that you are thinking of the expression as a sum of things, so when you have a difference you think of it as adding a negative, so for example the first of those polynomials should be thought of as x7+-3x+1. We just write such things as subtraction because that using less ink. (See How to Add, Subtract, Multiply, and Divide Integers for more about the arithmetic of pluses and minuses.) I will only be using integer coefficients in this article, but the only thing different about using other coefficients is that you have to know how to do the arithmetic for those kinds of numbers. There are some problems with fraction coefficients in my MathHelp problem set collection Polynomials, so you can download that if you want some practice with that.
The expressions being added together are called terms. So for the first example here the terms are x7, -3x, and 1. For the second example they are x and 5. For the third example they are 6x3, -7x2, 6x, and -9. The rest are left as exercises for the student.
The degree of a one variable polynomial is the highest power that occurs in it. If the polynomial is written in standard form, then this will be the power of the first term. The first term is also sometimes called the leading term. The degrees of my example polynomials are 7, 1, 3, 1, 17, 5, and 0. For the ones and zero here you need to remember that anything raised to the 1 power is itself and anything raised to the 0 power is 1. (See Integer Exponents.) For determining degree we regard the variable alone as it raised to the 1 power. If the polynomial is just a constant, that is a number, we can think of it as that constant multiplied by x0, since anything times 1 is itself. Anyway, what this all means is that polynomials that have variables, but no powers are degree 1 and constant polynomials, ones that are just numbers are degree 0.
Polynomials can be classified both by how many terms they have and by their degrees, particularly when these are small numbers. Here are some names that you may see used.
Number of Terms
1 - monomial2 - binomial
3 - trinomial
4 - quadrinomial
5 - quintinomial
You will hear and see the first three of these quite commonly. The next two are not quite so common. There are more for higher numbers as well, but they are not very often used.
Degrees
0 - constant1 - linear
2 - quadratic
3 - cubic
4 - quartic
5 - quintic
The same holds with these. Up through 2, you will hear them all the time. People seldom talk of degree 1 or 2 polynomials, they almost always call them linear or quadratic instead. For degree 3, cubic is pretty common too, but beyond that I just gave the names for your entertainment.
Addition
To add polynomials we just drop the parentheses and simplify by combining like terms. Combining like terms is just like any other combining like terms. It comes from the distributive property. (See Getting Rid of Parentheses.) Remember that like with any algebraic simplifying, everything you do comes from a small number of properties, and in this case those are the properties that I have listed in my articles Getting Rid of Parentheses and Simplifying Exponential Expressions. And that's pretty much it. Anything that can't be justified by one of those properties can't be done. Also remember that whenever it looks like there is no coefficient, it is a 1, because 1 times anything is itself. When you simplify polynomials you deal with the different powers of the variables just like they were different variables, so for example, 3x2+2x has no like terms, so it cannot be simplified any further, but 3x2+2x2 does have like terms and can be simplified to 5x2 by combining like terms. Don't be tempted to think that the exponents add. That's only for multiplying.Example 1:
Add the polynomials.(4x3+x2-2x+3)+(3x2+5x)
Solution:
=4x3+4x2+3x+3
Explanation:
Drop the parentheses and combine like terms. There is only one x3 term. For the x2 terms the first one has no coefficient, so we give it a 1 for a coefficient because 1 times anything is itself and combine it with the 3x2 to make 4x2. Then for the x terms we have -2x and 5x, which combine to 3x. Remember to always regard subtraction as addition of a negative. There is only one constant term, so nothing needs to be done with it.Subtraction
Subtraction is just a teeny bit harder than addition, but you must really pay attention to that teeny bit, because otherwise it will get you. Just like with other kinds of simplifying with parentheses, see Getting Rid of Parentheses, when you have a minus sign in front of a set of parentheses, to get rid of the parentheses you have to make sure and change the signs of every term in the parentheses. You can think of this as applying the distributive property to a multiplication by -1, since -1 times anything is its opposite. After you have changed all of the signs of the second polynomial everything else is just like addition.Example 2:
Subtract the polynomials.(3x2-5x-6)-(4x3-5x2+2x-3)
Solution:
=-4x3+8x2-7x-3
Explanation:
Change all of the signs of the second polynomial and drop the parentheses. Then we just combine like terms just like with addition. There is nothing to go with the -4x3. The 3x2 and the 5x2 add up to the 8x2. The -5x and the -2x make -7x. And the -6 and the 3 add to -3.Multiplication
Multiplication is a bit harder, because we have two operations going on, multiplication and addition. The polynomial is a sum of things, and we want to multiply two of these sums together, so we have to be a bit more careful about getting rid of the parentheses, because it involves changing the order of operation. With the parentheses the addition is being done first, but without them the normal order of operations rule says that the multiplication is being done first. With addition it was all one operation, so it didn't matter. What you end up doing in the end is multiplying all possible pairs, and in the multiplications you have to use the rules of exponents to simplify. (See Simplifying Exponential Expressions.)Example 3:
Multiply the polynomials.(3x+5)(3x-4)
Solution:
=9x2-12x+15x-20
=9x2+3x-20
Explanation:
We're multiplying all the possible pairs, where one factor comes from the first polynomials and the other comes from the second polynomials. A good way to keep track of this is to go through the terms of the first polynomial and multiply the first one by each of the terms in the second polynomial and then go to the second one and multiply it by each of the terms of the second polynomial, then go to the third one, etc., etc., until you use up all of the terms. If the polynomials just have two terms each (binomials) like we have here, then a good way to remember this is FOIL, which stands for firsts, outers, inners, lasts.To see why this multiplying all possible pairs works, you need to apply the distributive property twice, first treating the (3x+5) like one big strange symbol for a letter, and then splitting it up.
(3x+5)(3x-4)
=(3x+5)(3x)+(3x+5)(-4)
=(3x)(3x)+(5)(3x)+(3x)(-4)+(5)(-4),
so in the end we see that this does in fact give us all possible pairs. We don't have to do this double distributive property thing every time we multiply, though. We just have to multiply each pair, but it is useful for you to see it once to see that this too just comes from the basic properties of real numbers.
Then after we write down the products of each of the pairs, we have to use the properties of exponents to simplify each term. (See Simplifying Exponential Expressions.) We add the exponents and multiply the numbers.
Then after that there are often like terms to combine. Here we need to add the -12x and the 15x to get 3x.
Example 4:
Multiply the polynomials.(2x2+3x+5)(x2-2x-3)
Solution:
=2x4-4x3-6x2+3x3-6x2-9x+5x2-10x-15
=2x4-x3-12x2-19x-15
Explanation:
Here again we multiply all possible pairs, but since they have more than two terms, we can't remember it by FOIL anymore. We just go about systematically starting with the first term in the first polynomial and multiplying it by each of the terms in the second polynomial and then going to the next term and doing the same until we get through all of the terms. After that we need to simplify each term by multiplying the numbers and adding the exponents. Then we combine the like terms to get the final answer. You can see that particularly if you had a lot of terms in the polynomials this could get quite long, but unfortunately multiplication is just hard, and there really isn't any way around that. But there is a slightly better way to keep track of things, that we will be learning shortly.Polynomial Arithmetic and Natural Number Arithmetic
There is an interesting thing about polynomial arithmetic, and that is that it is really very similar to natural number arithmetic. It turns out that you can do all polynomial arithmetic using methods very similar to those you use for numbers, and often it makes it easy to keep track of things. (See How to Add, Subtract, Multiply, and Divide Natural Numbers.) Here is how you could do the above example using these methods.Example 1:
Add the polynomials.(4x3+x2-2x+3)+(3x2+5x)
Solution:
3x2+5x
4x3+4x2+3x+3
Explanation:
Just like with several place numbers, we add vertically. We treat the powers of the variables like place values and line up the like terms, leaving spaces for any powers that are missing. The only difference is that we don't have to do any carrying. This is a really good technique for when you have to add up several polynomials like in some of the exercises in algebra books. You can add them up just like column addition of numbers and just add up the coefficients and let the variables come along for the ride.Example 2:
Subtract the polynomials.(3x2-5x-6)-(4x3-5x2+2x-3)
Solution:
-4x3+5x2-2x+3
-4x3+8x2-7x-3
Explanation:
The same thing as with addition except that we first change the signs of all of the terms in the second polynomial. I suppose it would be more like what we do with numbers if we left the signs as is and subtracted the columns, but with plus and minus numbers to deal with I think you will make less mistakes if you do it this way. Then just like with addition, the like terms are all nicely lined up this way, so you just add down the columns and bring along the variables for the ride.Example 3:
Multiply the polynomials.(3x+5)(3x-4)
Solution:
3x-4
-12x-20
9x2+15x
9x2+ 3x-20
Explanation:
Multiplication is where this method is really helpful. We multiply like we do with several place numbers. With several place numbers you also multiply all possible pairs of the digits. With polynomials we can treat the terms just like the digits of numbers. And remember how when you multiply numbers, you indent when you go to the tens place. Well, if you do it here, all the like terms will nicely line up for you to combine, and you won't lose anything. Multiply the -4 times the 5. Then multiply the -4 times the 3x. Then go to the x's place and multiply the 3x times the 5 and the 3x times the 3x. Then add up just like with numbers and that will take care of the combining of like terms.Example 4:
Multiply the polynomials.(2x2+3x+5)(x2-2x-3)
Solution:
x2- 2x- 3
-6x2- 9x-15
-2x3-6x2-10x
2x4+3x3+5x2
2x4+ x3-7x2-19x-15
Explanation:
In a long multiplication like this we can really see the benefit of this method. Just like with multiplying two three place numbers, we first multiply everything by the -3. Then we indent and multiply everything by -2x. Then we indent again and multiply everything by the x2, and magically all of the like terms line up, and we can add to combine our like terms.Formulas
Since multiplication can be long and tedious it is helpful to have some formulas for multiplications that come up often. Here are the most commonly used ones.(A+B)(A-B)=A2-B2
(A+B)2=A2+2AB+B2
(A-B)2=A2-2AB+B2
They come up often enough that it is worth memorizing them, not just for multiplying, but for later things as well, like factoring and completing the square where it is helpful to be able to recognize forms like these. You derive these formulas by applying FOIL just once for each of the formulas and then you will never have to use FOIL for any expressions of their form. Instead you can just write down the answer by knowing the formula.
The reason the first one works is that whenever you multiply the sum and difference of the same thing, the inners and the outers cancel out, so you just get the firsts and the lasts. It goes like this.
A2 (firsts) -AB (outers)
+BA (inners) -B2 (lasts)
=A2-B2
Now that you know this formula, whenever you see a multiplication that is the sum and difference of the same thing, you can do it real quickly without going through FOIL, because we have already gone through it in the general case.
Example 5:
Multiply the polynomials.(x+5)(x-5)
Solution:
Explanation:
This fits into the pattern of the formula, since it is a sum and difference of the same things. Here A is x and B is 5. So we just write down the difference of the squares for the answer.Example 6:
Solution:
Explanation:
Same thing here. A is 2x, and B is 3. You just have to remember that to square a product you have to square both factors, so when you square 2x, you square both the 2 and the x.You can also impress your friends with some mental arithmetic tricks by using this formula, because formulas like this work for numbers as well. Suppose you want to multiply 21x19. The quick way to do it using this formula is to write it as
(20+1)(20-1).
Then it is a sum and difference, so you can use the formula, and it is
202-12
Both of those computations are easy to do mentally. We compute 202 by computing 22 and adding two zeros, so that gives us 400, and since 12 is 1, the answer is 399. You can do this to good effect whenever you can write the numbers as the sum and difference of the same numbers and those numbers are easy to square. The easy way to unsure that is to use numbers that are the same amount up and down from a multiple of 10, like 33x27, 55x45, or 62x58. For 33x27, you could see it as (30+3)(30-3), and that would mean you would just need to square 30 and square 3 and find the difference, which would be 900-9=891. With a little bit a practice you can get quite quick at this. 55x45 and 62x58 are left as exercises for the student.
The second and third formulas are important because they tell us how to multiply a binomial by itself. For this instead of canceling out, the outers and inners are the same, so they double up.
(A+B)(A+B)
=A2 (firsts) +AB (outers)
+BA (inners) +B2 (lasts)
=A2+2AB+B2
Example 7:
Multiply the polynomials.(x+3)2
Solution:
Explanation:
Sometimes it is helpful when dealing with formulas like these to think about what it says in words. What this formula says in words is that to square a sum, the first term of the answer is the square of the first term, the second term is double the product, and the third term of the answer is the square of the second term. The square of the first term is x2. The product of the two terms is 3x, and double that is 6x. The last term squared is 32=9.Example 8:
Multiply the polynomials.(3x2+2x)2
Solution:
Explanation:
Same thing here, the terms are just a little more complicated and you have to remember that when you square a product you square both its factors. The product is 6x3. When you double that you get 12x3.The third formula isn't really totally necessary, because subtraction is just adding the opposite, but it makes it easier, because then you don't have to use any negative numbers. You can see that it is true, by applying the second formula and realizing that the only effect that the minus sign will have is on the middle term, because in in the last term the negative number is getting squared, so that makes a positive number. But for the middle term you have a plus times a minus, so that is a minus. When you are apply this formula just make sure and not make it more difficult than it is by thinking of the second number as negative. The formula is given to allow you to only use positive numbers, so your A and B should be positive when you use it.
Example 9:
Multiply the polynomials.Solution:
Explanation:
Again I think it is helpful to think about it in words. The only difference between this and the last formula is that the middle term will be minus. Here A is 4x and B is 3. The sign of the middle term of the answer will always match that of the second term in the original. For the first term we square the first, that's 16x2, for the second term it is double the product. The product is 12x, and then we double that to get 24x, but we make it minus. The last term is the square of the second, so it is 32=9.Division
We can also divide polynomials pretty much like we divide numbers. We do it like long division of several place numbers. It is nicer in some ways, but nastier in others. Remember how when you do long division, you make an estimate by using just the first places, and how it sometimes doesn't work, and you have to raise it or lower it? Well, with polynomials you do sort of the same thing, except it always works. But the nastier thing is that with polynomials you have to deal with negative number subtraction sometimes, which makes it easy to make careless errors. To makes things simpler I'll first do an example that doesn't involve any negative numbers.Example 10:
Divide the polynomials.Solution:
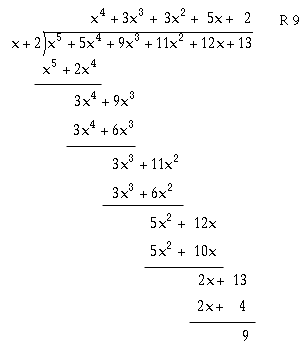
Explanation:
Okay, what we have here is x5+5x4+9x3+11x2+12x+13 loaves of bread that we want to give out to x+2 people, where x is some not yet specified number, and we want to figure out how many each person gets. (See How to Add, Subtract, Multiply, and Divide Natural Numbers and Egyptian Division.) We do it just like number long division, treating the terms like digits. Divide, multiply, subtract, bring down. Daddy, mommy, sister, brother, my 4th grade teacher taught us. If we were dividing 12 into 159123, we might get an idea of how many times 12 goes into 15 by asking how many times 1 goes into 1, and it would be 1. Similarly, here to get an idea of how many times x+2 goes into x5+5x4, we ask how many times does x go into x5. That means what can we multiply x by to get x5. That would be x4, so we write that down on the top. Not all textbooks recommend it, but I think it is a good idea to put it over the x4 term to keep track of the fact that we are really dividing x+2 into x5+5x4, just like if you were doing it with numbers you would put it over the 5 instead of the 1. That's the dividing step. Now we go to the multiplying. We were really dividing x+2 into x5+5x4, not just x into x5, so we multiply by the whole x+2 to check and find out how many loaves we have left after giving out x4 of them. To multiply the x4 times the x+2, we multiply it by the 2 and by the x, just like multiplying it by a two digit number. Then comes the subtraction. We subtract that from x5+5x4 to find out that we have 3x4 loaves left over from that part, but we also have the other terms, but we give out the bread that they represent a bit at a time to make sure we have enough for everyone, so we bring down just one more term, again just like it were a digit of a number.Now we want to divide x+2 into 3x4+9x3, and again we judge that by asking how many times x goes into 3x4. What can we multiply x by to get 3x4 ? That would be 3x3, so we write that on top. Next comes multiply, so we multiply that by x+2 to get 3x4+6x3. Subtract that and we get 3x3. Bring down the 11x2. That gives us 3x3+11x2.
Divide x+2 into 3x3+11x2 by asking how many times does x go into 3x3. That would be 3x2, so put that on the top. Multiply by the whole x+2 to get 3x3+6x2. Subtract that to get 5x2. Bring down the 12x to get 5x2+12x.
Divide x+2 into 5x2+12x by asking how many times does x go into 5x2. That would be 5x times, so put that on the top. Multiply it by the whole x+2 to get 5x2+10x. Subtract that to get 2x. Bring down the 13 to get 2x+13.
Divide x+2 into 2x+13 by asking how many times does x go into 2x. That would be 2 times, so put that on the top. Multiply it by the whole x+2 to get 2x+4. Subtract that to get 9, which is the remainder.
So that means that if we had x5+5x4+9x3+11x2+12x+13 loaves of bread that we wanted to give out to x+2 people, we could give out x4+3x3+3x2+5x+2 loaves to each person and have 9 left over.
It is a good idea to check a division problem like this by multiplying the answer by the divisor and adding the remainder. You should get the dividend (the thing you divided into) if you do that. This too is similar to what you would do with numbers. If you divided 59 by 7 and got 8 R 3, you could check this by multiplying 8 times 7 to get 56 and then adding 3 to get 59. Let's see if that works in this case. We can do this now with our polynomials using the vertical form of multiplication that we just learned about.
x4+3x3+3x2+ 5x+ 2
x+ 2
2x4+6x3+6x2+10x+4
x5+3x4+3x3+ 5x2+ 2x
x5+5x4+9x3+11x2+12x+4
9
x5+5x4+9x3+11x2+12x+13
Example 11:
Divide the polynomials.Solution:
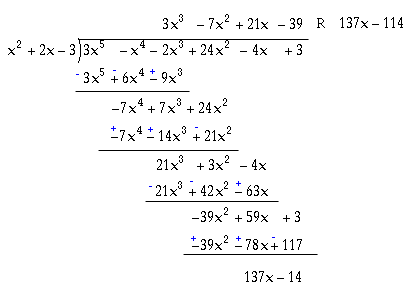
Explanation:
This one has some negative numbers and a 2nd degree polynomial for a divisor, so it is a little harder. But the procedure is still the same. For the negatives you just have to remember your integer arithmetic. (See How to Add, Subtract, Multiply, and Divide Integers for a review if you need it.) The subtractions in particular can easily lead to careless errors, so it is a good idea when doing them to right away change all of the signs of the bottom polynomial and then you can add instead of subtracting. But I have often found a problem with doing that, that it kind of looks bad when you want to go back and check your steps, because the multiplications look wrong, so my own tendency is to avoid it if I can. Also sometimes I am a little timid about suggesting the changing the signs and adding thing to students too soon, because it makes it sound too complicated, and it is too easy to forget that that it is really just the same procedure that you do with numbers. But on the other hand, most students don't have as much experience with plus and minus numbers as I do, so I find that if I don't tell them to change the signs and add, a lot of careless errors happen.Actually no matter what I do a lot of careless errors happen with polynomial long division. It is simply that sort of operation that is ripe with them. I have only found one way to deal with operations like that, and that is to SLOW DOWN. It's not a race. Nobody cares how fast you can do it. You are not going to be asked to do this on an assembly line. Machines can do this sort of thing a lot better than people can anyone. You are doing this sort of thing to get some hands on experience. We are not trying to drill you into being able to do it without thought. You are supposed to do these things WITH thought. You will learn a lot more if you do problems like polynomial long divisions slowly and accurately, even if it means that you don't do as many problems. The best kind of practice for problems like long division is to do a small number of problems, slowly and carefully. Everybody has their own way of working, but I find that when I have something I am doing that I want to make sure will be accurate and there are lots of places to make careless errors in it, it helps it I write really neat, and sometimes even take the time to write the lettering pretty and stylized--but that can be overdone--because it slows me down, makes me pay attention, to some extent maybe also keeps me from getting bored, and also makes it easier to check myself when I am done.
Anyway, getting back to the negatives and subtraction, after a bit of thought I came up with a compromise, which is that when changing the signs to add not to obliterate the original signs so that you can't tell what they were, but instead write the new signs for changing the subtractions into addition little and above the original signs. You might even want to try writing them in another color like I have done in the worked out division above, to make it really clear which are the originals and which are the changed ones. Also you don't really have to do it for every subtraction. Use your judgment. You know yourself better than I do. If you feel confident that you can do the subtraction without making sign errors, like particularly when everything is positive and the top numbers are bigger than the bottom numbers, then just do it as a subtraction. For example in this problem you might not want to bother with the 24 and the 21, because there it is easy enough to subtract 24-21, but I have written the changing of signs in there anyway. And no matter what, you can always think of it as a subtraction when you are remember the rules for the operations, so it really is still the same steps as with numbers. You just need to remember when you think of it this way that subtraction is adding the opposite, which shouldn't be a problem, because if you know your rules of plus and minus arithmetic, then you know that.
So getting down to the details of the problem, again we divide, multiply, subtract, and bring down. We see how many times x2+2x-3 goes into 3x5-x4-2x3 by asking ourselves how many times does x2 goes into 3x5, just like you would do if you were dividing 123 into 312443 and were judging how many times 123 goes into 312 by asking how many times 1 goes into 3. In the number case this wouldn't quite work this time, so you see that polynomials are in this way easier than numbers, because the 'estimate' always works here. The reason for that, by the way, is that numbers are more restrictive about what can be digits. The digits of numbers can only be 0 through 9, but coefficients can be anything, so all that matters with the polynomials is that the degree gets reduced, and that will happen as long as the first term is right. So we ask how many times x2 goes into 3x5, and that is 3x3, because 3x3 is the expression that you can multiply by x2 to get 3x5, so we write this on top and go on to the multiplying phase. Again like in the last example, we don't just multiply it by x2 , we multiply it by the whole divisor term by term to get 3x5+6x4-9x3. Then we subtract that from 3x5-x4-2x3. The safest way to subtract when you have a lot of minuses involved is to change all of the signs of the bottom polynomial and then add. I have indicated the new signs in blue, so we add using those signs and get -7x4+7x3. Then we bring down the 24x2.
Now we start the process again. Divide. How many times does x2 go into -7x4. That would be -7x2 times, so we put that on top. Multiply. Multiply -7x2 times x2+2x-3 to get -7x4-14x3+21x2. Subtract. To subtract this we change all of its signs and add it, which gives us 21x3+3x2. Bring down. Bring down the next term and we are ready for the next round.
Divide. How many times does x2 go into 21x3 ? 21x times, so we put that on the top. Multiply. We multiply that times x2+2x-3 to get 21x3+42x2-63x. Subtract. To subtract, change the signs of the bottom one and add. We get -39x2+59x. Bring down. Bring down the 3 and we are ready to do it one last time.
Divide. How many times does x2 go into -39x2. -39 times, so we put that on the top. Multiply. Multiply that by x2+2x-3 to get -39x2-78x+117. Subtract. To subtract we change all the signs of the bottom one and add, which gives us 137x-114. Nothing more to bring down, so that is our remainder.
Notice here that we have a remainder that is a linear expression, a 1st degree polynomial, instead of just a number. The rule is that the remainder must have degree less that the degree of the divisor, so this is okay since our divisor was degree 2.
Again we should check our answer by multiplying.
3x3-7x2+21x-39
x2+ 2x- 3
-9x3+21x2-63x+117
6x4-14x3+42x2-78x
3x5-7x4+21x3-39x2
3x5- x4- 2x3+24x2-141x+117
137x-114
3x5- x4- 2x3+24x2- 4x+ 3
Example 12:
Divide the polynomials(x6+x5-x2+2)÷(x3+x+2)
Solution:
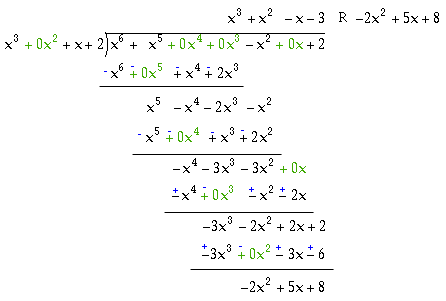
Explanation:
Here what's new is that there are some 'missing' terms, that is not all of the powers are there. When you do any of these operations with polynomials that have missing terms you need to either fill them in with terms with 0 coefficients or at least leave blanks for them and treat them as if they were terms with 0 coefficients. I have filled in with zeros for this one, but as you get more familiar with it, you may be able to get away with just leaving spaces. If you imagine what it would look like without the green parts, that is what it would look like if you did it with blanks.Then as usual you divide, multiply, subtract, and bring down, and again you can do your subtractions by changing all of the signs of the bottom one and adding and I have again indicated the new signs for that in blue. This time the remainder is degree 2, which is okay, because the divisor was degree 3.
Again we should always check, and with the multiplication we are also going to need spaces. For variety I will do it with spaces instead of zeros, since multiplication is a bit easier than division.
x3+ x2- x-3
x3 + x+2
2x3+2x2-2x-6
x4+ x3- x2- 3x
x6+ x5- x4-3x3
x6+ x5 + x2-5x-6
-2x2+5x+8
x6+ x5 + x2 +2
A Shorter Way
In spite of these more complicated examples I have given, really the most common use of long division is for simpler problems like the Example 5, but possibly involving some negatives. For problems like that there is shortcut method that you can check out if you'd like called synthetic division. You can find out about it by reading my article Synthetic Division.More Examples and Practice
To see some more examples and get more practice with the four operations of polynomial arithmetic see my MathHelp problem set collection Polynomials.