College Algebra
Tutorial 7:
Factoring Polynomials
 Learning Objectives Learning Objectives |
| After completing this tutorial, you should be able to: |
 Introduction Introduction |
| Factoring is to write an expression as a product offactors. For example, we can write 10 as (5)(2), where 5 and 2 are calledfactorsof 10. We can also do this with polynomial expressions. Inthis tutorial we are going to look at several ways to factor polynomialexpressions. By the time I'm are through with you, you will be afactoring machine. Basically, when we factor, we reverse the process of multiplyingthe polynomial which was covered in Tutorial 6: Polynomials. |
 Tutorial Tutorial |
| Greatest Common Factor (GCF) |
| The GCF for a polynomial is the largest monomialthat divides (isa factor of) each term of the polynomial. |
Step 1: Identifythe GCF of the polynomial.
Step 2: Dividethe GCF out of every term of the polynomial.
| This process is basically the reverse of thedistributive property. | |
 Example1: Factor out the GCF: Example1: Factor out the GCF: 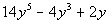 . . |
| Step 1: Identifythe GCF of the polynomial. |
| The largest monomial that we can factor out of eachterm is 2y. |
| Step 2: Dividethe GCF out of every term of the polynomial. |
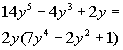 |
*Divide 2y outof every term of the poly. |
| Be careful. If a termof the polynomialis exactly the same as the GCF, when you divide it by the GCF you areleftwith 1, NOT 0. Don’t think, 'oh I have nothing left',there is actually a 1. As shown above when we divide 2yby 2y we get 1, so we need a 1 as thethirdterm inside of the ( ). Note that if we multiply our answer out, we should getthe originalpolynomial. In this case, it does check out. Factoringgivesyou another way to write the expression so it will be equivalent to theoriginal problem. |
 Example2: Factor out the GCF: Example2: Factor out the GCF: 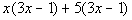 . . |
| This problem looks a little different, because now ourGCF is a binomial.That is ok, we treat it in the same manner that we do when we have amonomialGCF. Note that this is not in factored form because of theplus sign we havebefore the 5 in the problem. To be in factored form, it must bewrittenas a product of factors. |
| Step 1: Identifythe GCF of the polynomial. |
| This time it isn't a monomial but a binomial that wehave in common. Our GCF is (3x -1). |
| Step 2: Dividethe GCF out of every term of the polynomial. |
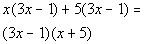 |
*Divide (3x-1) out of both parts |
| When we divide out the (3x- 1) out ofthe first term, we are left with x. Whenwe divide it out of the second term, we are left with 5. That is how we get the (x +5) for our second( ). |
Factoring a Polynomial with
Four Terms by Grouping |
In some cases there is not a GCF for ALL the termsin a polynomial. If you have four terms with no GCF, then try factoring by grouping.
Step 1: Groupthe firsttwo terms together and then the last two terms together.
Step 2:Factor out a GCFfrom each separate binomial.
Step 3:Factor out thecommon binomial. |
 Example3: Factor by grouping: Example3: Factor by grouping: 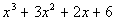 . . |
| Note how there is not a GCF for ALL the terms. Solet’s go aheadand factor this by grouping. |
| Step 1:Group the firsttwo terms together and then the last two terms together. |
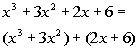 |
*Two groups of two terms |
| Step 2: Factorout aGCF from each separate binomial. |
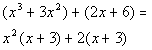 | *Factor out an x squaredfrom the 1st ( )
*Factor out a 2 from the 2nd( ) |
| Step 3:Factor out thecommon binomial. |
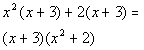 |
*Divide (x+ 3)out of both parts |
| Note that if we multiply our answer out, we do get theoriginal polynomial. |
 Example4: Factor by grouping: Example4: Factor by grouping: 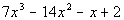 . . |
| Note how there is not a GCF for ALL the terms. Solet’s go aheadand factor this by grouping. |
| Step 1:Group the firsttwo terms together and then the last two terms together. |
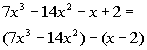 |
*Two groups of two terms |
| Be careful. Whenthe firstterm of the second group of two has a minus sign in front of it, youwantto put the minus in front of the second ( ). When youdo this you need to change the sign of BOTH terms of the second ( ) as shown above. |
| Step 2: Factorout aGCF from each separate binomial. |
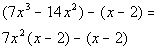 | *Factor out a 7x squaredfrom the 1st ( )
*Nothing to factor out from the2nd ( ) |
| Step 3:Factor out thecommon binomial. |
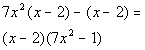 |
*Divide (x- 2)out of both parts |
| Note that if we multiply our answer out that we do getthe originalpolynomial. |
| FactoringTrinomials ofthe Form 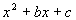
(Where the number in front of xsquared is 1) |
| Basically, we are reversing the FOIL method to getour factoredform. We are looking for two binomials that when you multiplythemyou get the given trinomial. Step 1:Set up a productof two ( ) where each will hold two terms.
| It will look like this: ( )( ). |
Step 2:Find the factorsthat go in the first positions.
| To get the xsquared (which is the F inFOIL), we would have to have an x inthe firstpositions in each ( ). So it would look like this: (x )(x ). |
Step 3: Find thefactors that go in the last positions.
| The factors that would go in the last positionwould have to be twoexpressions such that their product equals c(the constant) and at the same time their sum equals b(number in front of x term). As you are finding these factors, you have toconsider the sign of theexpressions:
| If c is positive,your factors are going to both have the same sign depending on b’ssign. If c is negative,your factors are going to have opposite signs depending on b’ssign. | | |
 Example5: Factor the trinomial: Example5: Factor the trinomial: 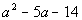 . . |
| Note that this trinomial does not have a GCF. So we go right into factoring the trinomial of theform 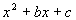 . . |
| Step 1: Setup a productof two ( ) where each will hold two terms. |
| It will look likethis: ( )( ) |
| Step 2: Findthe factorsthat go in the first positions. |
| Since we have a squaredas our first term,we will need the following: (a )(a ) |
| Step 3: Findthefactors that go in the last positions. |
| We need two numbers whose product is -14 and sum is-5. Thatwould have to be -7 and 2. Putting that into our factors we get: |
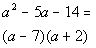 |
*-7 and 2 are two numbers whoseprod. is -14
and sum is -5 |
| Note that if we would multiply this out, we would getthe originaltrinomial. |
 Example6: Factor the trinomial: Example6: Factor the trinomial: 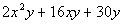 . . |
| Note that this trinomial does have a GCF of 2y. We need to factor out the GCF beforewe tackle the trinomial part of this. |
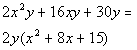 |
*Factor out the GCF of 2y |
We are not finished, we can still factor thetrinomial. It isof the form 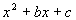 . . Anytime you are factoring, you need to make sure thatyou factor everythingthat is factorable. Sometimes you end up having to do severalstepsof factoring before you are done. |
| Step 1(trinomial): Setup a product of two ( ) where each will hold two terms. |
| It will look like this: 2y( )( ) |
| Step 2(trinomial): Findthe factors that go in the first positions. |
| Since we have x squared as our first term, we will needthe following: 2y(x )(x ) |
| Step 3(trinomial): Find the factors that go in the last positions. |
| We need two numbers whose product is 15 and sum is8. Thatwould have to be 5 and 3. Putting that into our factors we get: |
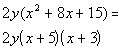 |
*5 and 3 are two numbers whoseprod. is 15
*and sum is 8 |
| Note that if we would multiply this out, we would getthe originaltrinomial. |
| Factoring Trinomials of the Form 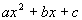
(where a does notequal 1) |
| Again, this is the reverse of the FOIL method. The difference between this trinomial and the onediscussed above, isthere is a number other than 1 in front of the xsquared. This means, that not only doyouneed to find factors of c, but also a.
Step 1: Set up aproduct of two ( ) where each will hold two terms.
| It will look like this( )( ) |
Step 2:Use trial anderror to find the factors needed.
| The factors of a willgo in the firstterms of the binomials and the factors of cwill go in the last terms of the binomials. The trick is to get the right combination of thesefactors. Youcan check this by applying the FOIL method. If your product comesout to be the trinomial you started with, you have the rightcombinationof factors. If the product does not come out to be the giventrinomial,then you need to try again. | |
 Example7: Factor the trinomial Example7: Factor the trinomial 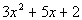 . . |
| Note that this trinomial does not have a GCF. So we go right into factoring the trinomial of theform 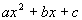 . . |
| Step 1: Set upa product of two ( ) where each will hold two terms. |
| It will look like this: ( )( ) |
| Step 2:Use trial anderror to find the factors needed. |
| In the first terms of the binomials, we need factorsof 3 xsquared. This would have to be 3x and x. In the second terms of the binomials, we need factorsof 2. This would have to be 2 and 1. I used positives here because themiddle term is positive. Also, we need to make sure that we get the rightcombination of thesefactors so that when we multiply them out we get 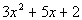 . . |
| Possible Factors | Check using the FOILMethod | First try:
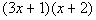
| 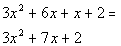 This is not our original polynomial. So we need to try again.
| Second try:
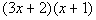
| 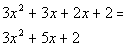
This is our original polynomial. So this is the correct combination of factors forthis polynomial.
|
| This process takes somepractice. Aftera while you will get used to it and be able to come up with the rightfactoron the first try. |
 Example8: Factor the trinomial Example8: Factor the trinomial 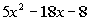 . . |
| Note that this trinomial does not have a GCF. So we go right into factoring the trinomial of theform 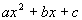 |
| Step 1: Set upa product of two ( ) where each will hold two terms. |
| It will look like this: ( )( ) |
| Step 2: Usetrial anderror to find the factors needed. |
| In the first terms of the binomials, we need factorsof 5 x squared.This would have to be 5x and x. In the second terms of the binomials, we need factorsof -8. This would have to be -8 and 1, 8 and -1, 2 and -4, or -2 and 4. Since the product of these factors has to be a negative number, we needone positive factor and one negative factor. Also we need to make sure that we get the rightcombination of thesefactors so that when we multiply them out we get 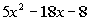 . . |
| Possible Factors | Check using the FOILMethod | First try:
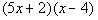
| 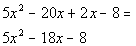 This is our original polynomial. So this is the correct combination of factors forthis polynomial.
|
| Not every polynomial is factorable. Just like notevery numberhas a factor other than 1 or itself. A prime number is a numberthathas exactly two factors, 1 and itself. 2, 3, and 5 are examplesofprime numbers. The same thing can occur with polynomials. Ifa polynomialis not factorable we say that it is a prime polynomial. Sometimes you will not know it is prime until you startlooking forfactors of it. Once you have exhausted all possibilities, thenyoucan call it prime. Be careful. Do not think because youcould not factor it on the first try that it is prime. You mustgothrough ALL possibilities first before declaring it prime. |
 Example9: Factor the trinomial Example9: Factor the trinomial 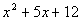 . . |
| Note that this trinomial does not have a GCF. So we go right into factoring the trinomial of theform 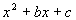 . . |
| Step 1:Set up a productof two ( ) where each will hold two terms. |
| It will look likethis: ( )( ) |
| Step 2: Findthe factorsthat go in the first positions. |
| Since we have x squaredas our first term,we will need the following: (x )(x ) |
| Step 3: Find thefactors that go in the last positions. |
| We need two numbers whose product is 12 and sum is 5. Can you think of any???? Since the product is a positive number and the sum isa positivenumber, we only need to consider pairs of numbers where both signs arepositive. One pair of factors of 12 is 3 and 4, which does notadd up to be 5.
Another pair of factors are 2 and 6, which also does notadd upto 5.
Another pair of factors are 1 and 12, which also doesnot add upto 5. Since we have looked at ALL the possible factors, andnone of themworked, we can say that this polynomial is prime. In other words, it does not factor. |
| Factoringa Perfect SquareTrinomial 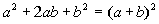
OR
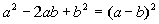
|
| It has to be exactly in this form to use thisrule. When youhave a base being squared plus or minus twice the product of the twobasesplus another base squared, it factors as the sum (or difference) of thebases being squared. This is the reverseof thebinomial squared found in Tutorial 6: Polynomials. Recallthat factoring is the reverse of multiplication. |
 Example10: Factor the perfect square trinomial: Example10: Factor the perfect square trinomial: 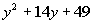 . . |
| First note that there is no GCF to factor out of thispolynomial. Since it is a trinomial, you can try factoring this bytrial and error shown above. But if you can recognizethatit fits the form of a perfect square trinomial,you can save yourself some time. |
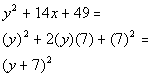 |
*Fits the form of a perfect sq.trinomial
*Factor as the sum of bases squared |
| Note that if we would multiply this out, we would getthe originalpolynomial. |
 Example11: Factor the perfect square trinomial: Example11: Factor the perfect square trinomial: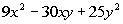 . . |
| First note that there is no GCF to factor out of thispolynomial. Since it is a trinomial, you can try factoring this bytrial and error shown above. But if you can recognizethatit fits the form of a perfect square trinomial,you can save yourself some time. |
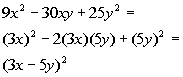 |
*Fits the form of a perfect sq.trinomial
*Factor as the diff. of basessquared |
| Note that if we would multiply this out, we would getthe originalpolynomial. |
| Factoringa Difference ofTwo Squares 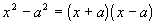
|
| Note that the sum of twosquares DOES NOTfactor. Just like the perfect square trinomial, the differenceof two squares has to be exactly in this form to use this rule. Whenyouhave the difference of two bases being squared, it factors as theproductof the sum and difference of the bases that are being squared. This is the reverseof theproduct of the sum and difference of two terms found in Tutorial 6:Polynomials. Recall that factoring is the reverse of multiplication. |
 Example12: Factor the difference of two squares: Example12: Factor the difference of two squares: 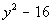 . . |
| First note that there is no GCF to factor out of thispolynomial. This fits the form of a the differenceof two squares. So we will factor using that rule: |
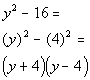 |
*Fits the form of a diff. of twosquares
*Factor as the prod. of sum anddiff. of bases |
| Note that if we would multiply this out, we would getthe originalpolynomial. |
 Example13: Factor the difference of two squares: Example13: Factor the difference of two squares: 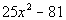 . . |
| First note that there is no GCF to factor out of thispolynomial. This fits the form of the differenceof two squares. So we will factor using that rule: |
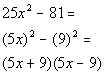 |
*Fits the form of a diff. of twosquares
*Factor as the prod. of sum anddiff. of bases |
| Note that if we would multiply this out and theoriginal expressionout we would get the same polynomial. |
| Factoringa Sum of Two Cubes 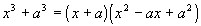
|
| The sum of two cubes has to be exactly in thisform to use thisrule. When you have the sum of two cubes, you have a productofa binomial and a trinomial. The binomial is the sum of the basesthat are being cubed. The trinomial is the first base squared,thesecond term is the opposite of the product of the two bases found, andthe third term is the second base squared. |
 Example14: Factor the sum of cubes: Example14: Factor the sum of cubes: 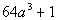 . . |
| First note that there is no GCF to factor out of thispolynomial. This fits the form of thesum of cubes. So we will factor using that rule: |
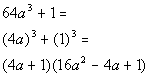 | *Fits the form of a sum of twocubes
*Binomial is sum of bases
*Trinomial is 1st base squared,minus prod.of bases, plus 2nd base squared |
| Note that if we would multiply this out, we would getthe originalpolynomial. |
| Factoringa Difference ofTwo Cubes 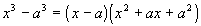
|
| This is factored in a similar fashion to the sum of twocubes. Note the only difference is that the sign in the binomial is a - whichmatches the original sign, and the sign in front of ax is positive,whichis the opposite sign. The difference of two cubes has to be exactly in thisform to use thisrule. When you have the difference of two cubes, you have aproductof a binomial and a trinomial. The binomial is the difference ofthe bases that are being cubed. The trinomial is the first basesquared,the second term is the opposite of the product of the two bases found,and the third term is the second base squared. |
 Example15: Factor the difference of cubes: Example15: Factor the difference of cubes: 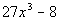 . . |
| First note that there is no GCF to factor out of thispolynomial. This fits the form of thedifference ofcubes. So we will factor using that rule: |
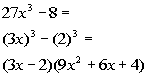 | *Fits the form of a diff. oftwo cubes
*Binomial is diff. of bases
*Trinomial is 1st base squared,plus prod.of bases, plus 2nd base squared |
| Note that if we would multiply this out, we would getthe originalpolynomial. |
| Now that you have a list of different factoring rules,let’s put itall together. The following is a checklist of the factoring rulesthat we have covered in our tutorials. When you need to factor, youALWAYS look forthe GCF first. Whether you have a GCF or not, thenyou continue looking to see if you have anything else thatfactors. Below is a checklist to make sure you do not missanything. Alwaysfactor until you can not factor any further. |
| Factoring Strategy I. GCF:
| Always check for the GCF first, no matter what. | II. Binomials:
III. Trinomials:
IV. Polynomials with four terms:
|
 Example16: Factor Example16: Factor 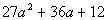 completely. completely. |
| The first thing that we always check when we arefactoring is WHAT? The GCF. In this case, there is one. Factoring out the GCF of 3 we get: |
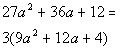 |
*Factor a 3 out of every term |
| Next, we assess to see if there is anything else thatwe can factor. We have a trinomial inside the ( ). It fits the formof a perfect square trinomial, so we willfactorit accordingly: |
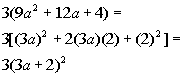 |
*Fits the form of a perfect sq.trinomial
*Factor as the sum of bases squared |
| There is no more factoring that we can do in thisproblem. Note that if we would multiply this out, we would getthe original polynomial. |
 Example17: Factor Example17: Factor 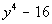 completely. completely. |
| The first thing that we always check when we arefactoring is WHAT? The GCF. In this case, there is not one. So we assess what we have. It fits the form of a differenceof two squares, so we will factor it accordingly: |
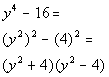 |
*Fits the form of a diff. of twosquares
*Factor as the prod. of sum anddiff. of bases |
| Next we assess to see if there is anything else that wecan factor. Note how the second binomial is another differenceof two squares. That means we have to continue factoringthis problem. |
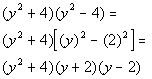 |
*Fits the form of a diff. of twosquares
*Factor as the prod. of sum anddiff. of bases |
| There is no more factoring that we can do in thisproblem. Note that if we would multiply this out, we would getthe original polynomial. |
 Example18: Factor Example18: Factor 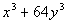 completely. completely. |
| The first thing that we always check when we arefactoring is WHAT? The GCF. In this case, there is not one. So we assess what we have. It fits the form of a sumof two cubes, so we will factor it accordingly: |
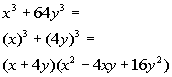 |
*Fits the form of a sum of twocubes
*Binomial is sum of bases
*Trinomial is 1st base squared,minus prod.of bases, plus 2nd base squared |
| There is no more factoring that we can do in thisproblem. Note that if we would multiply this out, we would getthe original polynomial. |
 Example19: Factor Example19: Factor 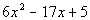 completely. completely. |
| The first thing that we always check when we arefactoring is WHAT? The GCF. In this case, there is not one. So we assess what we have. This is a trinomial that doesnot fit theform of a perfect square trinomial. Looks like we will have touse trialand error: |
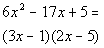 |
*Factor by trial and error |
| There is no more factoring that we can do in thisproblem. Note that if we would multiply this out, we would getthe original polynomial. |
 Example20: Factor Example20: Factor 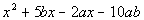 completely. completely. |
| The first thing that we always check when we arefactoring is WHAT? The GCF. In this case, there is not one. So we assess what we have. This is a polynomial withfour terms. Looks like we will have to try factoring it bygrouping: |
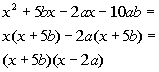 |
*Group in two's
*Factor out the GCF out of eachseparate ( )
*Factor out the GCF of (x+ 5b) |
| There is no more factoring that we can do in thisproblem. Note that if we would multiply this out, we would getthe original polynomial. |
 Practice Problems Practice Problems |
| These are practice problems to help bring you to thenext level. It will allow you to check and see if you have an understanding ofthesetypes of problems. Math works just likeanythingelse, if you want to get good at it, then you need to practiceit. Even the best athletes and musicians had help along the way and lots ofpractice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice. To get the most out of these, you should work theproblem out onyour own and then check your answer by clicking on the link for theanswer/discussionfor that problem. At the link you will find the answeras well as any steps that went into finding that answer. |
 PracticeProblems 1a - 1f: PracticeProblems 1a - 1f: Factor completely. |
1a. 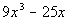
(answer/discussionto 1a) | 1b. 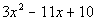
(answer/discussionto 1b) |
1c. 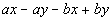
(answer/discussionto 1c) | 1d. 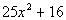
(answer/discussionto 1d) |
1e. 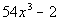
(answer/discussionto 1e) | 1f. 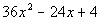
(answer/discussionto 1f) |
 Need Extra Help on These Topics? Need Extra Help on These Topics? |
The following are webpagesthat can assistyou in the topics that were covered on this page:
int_alg_tut27_gcf.htm
This webpage goes over how to factor out a GCF and how to factor bygrouping.
This webpage helps you with factoring out the GCF.
This webpage will help you with factoring out the GCF.
factoring/gcf.html
This webpage will help you with factoring out the GCF.
factoringgrouping.htm
This webpage will help you with how to factor by grouping.
int_alg_tut28_facttri.htm
This webpage goes over how to factor trinomials.
This webpage helps you factor trinomials.
This website helps you factor trinomials.
This website helps you factor trinomials.
int_alg_tut29_specfact.htm
This webpage goes over how to factor perfect square trinomial,differenceof squares, and sum or difference of cubes.
This webpage helps you with the factoring by special products discussedin this tutorial.
This webpage helps you with the factoring by special products discussedin this tutorial. |
forsomemore suggestions. |
All contents
June 22, 2003 |