While Mr. Johnson is meeting with some of the children in hisfirst-grade class, others are involved in a number of differentactivities. At the Math Center, pairs of students have cups witheleven chips that are yellow on one side and red on the other. As eachpair pours out the chips, they write a number sentence showing howmany yellows and how many reds they got, as well as the total. Whenthey have written ten number sentences each, they move on to anotheractivity.

The students:

work on basic facts in the context of a problem and in relationto other areas of mathematics.

work in pairs with manipulatives.

Later in the day, as Mr. Johnson begins the math lesson, he asksthe students to recall their discussion from the previous day,"What were we talking about yesterday in math?"

practice their number facts by writing down eachresult.

"We were doing numbers that add up to eleven, like 5+6and 2+9," answers Clark.

"Or 3+8 and 4+7," adds Sarah.

"Is there more than one way to get a sum of eleven?"

share mathematical ideas.

Mr. Johnson lists all of the children's responses on the board. Hegoes on to ask them, "What were you doing at the Math Centerearlier today?"

Jackie responds, "We were tossing counters and writing numbersentences."

"We were tossing eleven counters!" says Toni.

"What can you tell me about your results?" asksMr. Johnson. "Did you get the same number sentences as yourpartner?"

"No - we got different ones!"

connect their understanding of one mathematical idea toanother.

"Our answers were always the same - eleven!"

"I got some number sentences more than once!"

"I got 5+6 three times!"

"I didn't get 0+11 or 11+0 at all!"

report and reflect on the differences of their results.

"Why do you think you got different answers?" asksMr. Johnson. He listens as the students talk about fairness, luck, andchance, pointing out that all of the counters are alike. The studentsagree finally that the different number sentences are a result ofchance.

The students continue their discussion of which number sentencesappear more often than others. One of the children suggests that maybethey should make a graph to help them see which number sentences occurmost often. Mr. Johnson thinks that this is a good idea. He goesthrough their list of number sentences, asking students to raise onefinger if they got that number sentence once, two fingers if they gotit twice, and so on. For each finger raised, he puts a tally mark onthe board. When they are done, he asks whether there were any othernumber sentences that anyone got. Then the children look at thegeneral shape of the data, noticing that most of the number sentenceswere in the middle. Mr. Johnsonpoints out that not all of the numbersentences are equally likely to occur. He says that tomorrow they willhave a chance to play a game with the counters in which they willneed to select which number sentences will be winners. Tomorrow'sactivity will continue providing opportunities for practicing basicfacts while building on the beginning ideas of probability.

informally explore the concepts of probability.

use different methods to display data.

make inferences about their data.

Mr. Marshall had assigned the following problem from the New JerseyEarly Warning Test as a homework assignment for his fourth gradeclass:

The students:

are asked to respond to open-ended questions and present anddefend their solutions.

The students were to solve the problem and match their responsewith that of Tilly Tester to see if they agree or disagree withTilly's response and explain why.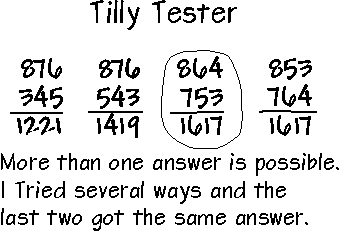

are asked to analyze problems for reasonableness of results andto diagnose errors.

As the math class begins, Mr. Marshall allows the students to workin the cooperative learning groups which they have been working withthis month to compare the results of their homeworkassignment. Mr. Marshall visits each group noting who has completedthe assignment as well as the direction of the discussion for eachgroup. Homework assignments are important and students are givencredit for homework. Strategies such as displaying answers on theoverhead projector and working in cooperative learning groups are usedto ensure that homework review is no more than 5 to 10 minutes.

work cooperatively to assess their own and each other'swork.

Mr. Marshall then asks the students to show the level of theiragreement with Tilly's response on a 0-5 scale, with 0 signifyingdisagreement and 5 signifying total agreement. Most students raise 4or 5 fingers, and the discussion then focuses on how Tilly's answercould be improved. One group notes that Tilly should have added eachpair of numbers and shown the sum for each, while another groupexplains that Tilly could have also changed the hundreds place to get754+863 and 763+854.

are willing to take a position without the fear of beingincorrect.

At this point, Mr. Marshall discusses Tilly's understanding ofplace value and uses the opportunity to summarize the students'responses and lead into the objective of the day which focuses onplace value and multiplication.

use their knowledge of numeration to help solveproblems.

"Let's work on multiplication today, and to get started, let'sdo some mental math with multiplication. On the back of your homework,number 1 to 10. Write the answers only for my mental mathflashcards."

Individually, the students write answers for 8000x3, 6000x7+50,300x7, etc. After the ten problems, Mr. Marshall has the studentsexchange papers, and they correct and discuss the answers. The papersare collected, and Mr. Marshall poses the following problem for hisstudents:

Use four of these five digits and construct the multiplicationproblem that gives the greatest product: 1, 3, 5, 7, 9

use mental math regularly throughout the curriculum.

demonstrate their understanding of mathematical concepts in avariety of ways, each of which provides valuable assessmentinformation to the teacher.

Before allowing the students to start work on the problem, he asksthem to estimate what the largest product obtained in this mannermight be. Students offer estimates ranging from 3000 to 10,000 andprovide explanations for their guesses. When allowed to, the classworks in their cooperative learning groups. Calculators areavailable, and some students start guessing and checking with theircalculators.

are encouraged to estimate solutions before actually determininganswers.

use calculators to aid in the problem-solving process.

One group begins to discuss which digits to use, wondering whetherthere would be a reason not to use the four largest digits. Anothergroup is discussing whether a 2-by-2 or a 1-by-3 arrangement would bethe best for getting a large product, an aspect of the problem thatsome groups have completely missed. Most of the groups get around totrying out sample problems of a variety of sorts to get someparameters worked out. Toward the end of the class session, thegroups share the specific answers they have come up with. The threeexamples that are suggested are:

    753    93    953  x   9  x 75  x   7  -----  ----  -----   6777  6975   6671

using mathematical reasoning to formulate strategies andsolutions.

It is clear to everyone that the 2-by-2 digit problem is the onewith the greatest product, but Mr. Marshall is looking for somegeneralizations that can be made. He points out that none of thegroups used the digit "1" in their examples. Can thelowest digit always be ruled out? He asks the groups that arrivedat the 2-digit problem to explain how they decided where to put theindividual digits. Does it matter where they were placed?Where does the largest one go? The smallest? Do you think it wouldalways work that way regardless of what the individual digitswere? How can you check? The students reflexively pick up theircalculators and begin to formulate other versions of the problem thatuse other digits and to check which arrangements of the digits givethe largest product. One student asks his partners what they thinkwould happen if two or three digits were the same.

approach numerical operations from a holistic point of viewrather than only through paper-and-pencil manipulation.

For homework, Mr. Marshall asks the students to use the same fivedigits, but to find the smallest possible product. They are then towrite a paragraph describing their solution and the reasoning theyused to show it is, indeed, the smallest product. Specifically, theyare to consider the question: Can you just turn yourthinking about the way you got the largest product upside down and useit to get the smallest product?

write paragraphs describing and justifying theirpositions.

Today is November 12 and Maria, a student in Miss Palmer'ssecond grade class is very excited. Today is Maria's birthday,and as is the custom in her class, she is bringing in a birthday snackto share with her classmates. Maria and her father spent much of theprevious evening making a batch of chocolate chip cookies and sheproudly walks into class carrying a cannister full to the brim. MissPalmer realizes that she can use mathematics to help the class dividethe cookies.

Before the afternoon snack time, Miss Palmer poses the problem tothe whole class.

The students:

use mathematics to devise a solution for real-worldproblems.

Miss Palmer states, "Today is Maria's birthday and shehas brought in some delicious chocolate chip cookies for all of us toenjoy at snack time. Maria told me she baked a whole bunch ofcookies. I would like us to think about how we could determine thenumber of cookies each student in the class should get. Discuss itwith your partner."

use cooperative work to generate potential solutions.

The students begin to discuss all of their ideas. After a fewminutes, Miss Palmer calls on a few of the students. As they sharetheir ideas, the teacher records them on the language experiencechart.

Sarah states, "Well, me and Mario think that the first thingwe have to do is count the cookies to find out how many thereare."

Jerome adds, "Yeah, and we also need to know how many childrenare in the class today."

"That's easy. I did the lunch count this morning and thereare 22 children in school today," Maria volunteers.

Luis chimes in. "Once we know how many cookies and how manychildren, then we can figure out a way to solve the problem."

The children all agreed that since they know there are 22 childrenin class today, the next step was to determine the number of cookies.Miss Palmer highlights that idea on the language experience chart andgives each pair of children a bag of counters which represents thenumber of cookies.

regularly share their ideas publicly.

Miss Palmer says, "Each pair of children received a bag ofcounters. I want you to pretend that these are Maria's cookies. I'vecounted the cookies. The number of counters in each bag is equal tothe number of cookies Maria brought for a snack. With your partner,use your counters to first decide how many cookies Maria brought toschool and then determine how many cookies each student will get ifthe cookies are to be shared equally among everyone in the class.When you are finished, each pair will need to write a story whichexplains how both of you solved the problem."

use manipulatives to model real-world situations.

The children worked with their regular partners. The first taskthey all tackled was to count the number of counters in each bag.Most of the pairs of children counted by twos to determine the totalnumber of counters was 62. However, Alex and Laura kept losing countwhen trying to count all the counters and decided to group thecounters by ten. Miss Palmer was delighted to see that most pairs ofchildren had written the total number of counters (62) on a sheet ofpaper. She had been stressing the importance of collecting data andrecording information.

As Miss Palmer continued to circulate around the classroom, shenoticed the children were solving thesharing problem in variousways.

use their knowledge of decimal place value to simplify thetask.

One pair of students begins by drawing 22 stick figures to standfor the students in the class and then starts to "give out"the cookies by drawing them in their stick figures' hands. Anotherpair also starts with 22 stick figures but then draws 62 littlecookies on another part of the paper and is stumped about where to gofrom there. Mario and Sarah begin to sort the 62 counters into 22piles. Another pair, trying to use calculators to solve the problem,starts by adding 22 cookies for everyone to another 22 cookies foreveryone to a third 22 cookies for everyone and then realizes thatthey have exceeded the number of cookies available.

Miss Palmer, noticing that the students will be unable to finishthe problem before they have to go to Physical Education, calls thestudents back together.

"I want all of you to stop what you are doing, and with yourpartner write a story to tell me how you are attempting to solve thisproblem," she directs.

develop their own methods for solving the problem.

use technology as a problem-solving tool.

The students eagerly write their stories. Some use pictures tohelp illustrate their solutions.

Miss Palmer requests, "I would like some of the pairs toreport to the whole class how they were attempting to solve theproblem."

draw pictures to model their solutions.

Luis states, "Well, Elizabeth and I figured out that eachstudent could have 2 cookies and there will be 18 cookies left. Weknow this because we drew a picture of the class and put counters oneach student. When we couldn't give counters to every kid, we decidedthose were leftovers and we counted them."

Lisa volunteers, "We drew stick figures too. After we gaveout 2 cookies to each child, Jerome said we couldn't give out the 18leftovers. But I think we can break the leftover cookies in half.Then each child would get 2 whole cookies and one half cookie. ButI'm not sure how many would be left over then."

"Sarah and I used the calculator to solve the problem. We putin 62 and I counted while Sarah subtracted 22. We got 2 with 18 leftover," Mario added.

"Alex and I got a different answer. We used the counters andput them into 22 piles, but we got 17 leftovers," Laura said.

Lisa suggested, "Maybe you and Alex should count them again tomake sure you have the right number in each pile."

give explanations of their strategies for solving theproblem.

informally explore the uses of fractions and notions of fairsharing.

Laura and Alex recount their piles and discover that one counterfell on the floor.

Vanessa states, "Me and my partner thought of another way ofsharing the leftover cookies. Everyone could write their name on apiece of paper, then put all the papers into a bag and have Mariaclose her eyes and pick out 18 names. Those kids would get the extracookies."

Sarah protested, "We forgot about Miss Palmer. We should giveher 2 cookies and that would leave 16 left over. Maria could givethem to the principal and the other ladies in the office."

Miss Palmer wrapped up the discussion. "We've discussed manyideas for sharing the 62 cookies Maria brought for a snack. On theback of the sheet of paper I gave you, I would like you and yourpartner to decide on how you think we could fairly share thecookies."

are mutually supportive and regularly offer feedback to eachother.

The children work on their final summary of the problem and handtheir papers in before getting on line for Physical Education. Whilethe children are in Physical Education, Miss Palmer reads thechildren's solutions. She makes notes on the cards she keeps foreach child. This will help her better understand variousdevelopmental levels of her students. She notices that Vanessa hasreally made progress since September. Laura and Alex still like to"rush" to finish their work. She makes a note on theirpaper encouraging them not to be so concerned about being the firstones finished. Overall, she feels encouraged, not only about thesolutions to the problems, but also about the ways in which her classhas learned to communicate their ideas both orally and on paper. Shedecides to let the class choose one of the methods suggested todistribute the cookies at snack time.

demonstrate their understanding of mathematical concepts in avariety of ways, each of which provides valuable assessmentinformation to the teacher.

Mr. Santos' 6th grade class has just completed a review of placevalue in the decimal number system and he is preparing to start a unitintroducing exponents. He has coordinated the timing of this unitwith the language arts teacher whose class is in the midst of a uniton fables. One fable they have read involves a knight who saves akingdom from a horrendous dragon. Given the opportunity to determinehis own reward, he tells the king that he would take one penny on thefirst square of a chessboard, two pennies on the second, four pennieson the third, and so forth until each square on the chessboard hastwice as many as the previous one. Mr. Santos has the students recallthe story and then asks the students to determine how much money theknight would make with this method of payment.

The students:

are connecting a language arts experience to their mathematicslearning.

Mary said, "We need to know how many squares there are on achessboard before we can do this problem."

are comfortable taking risks.

Lionel stated, "Give me a minute to think. I play on thechess team, but I need to take a moment to picture it. Let's see, Iknow it's square and there are 1,2,3, ...8 squares along the one side.There are 64 squares!"

Jerry shouted, "He gets 128 pennies. Two on eachsquare."

use known facts to explain their thinking.

"The fable doesn't say he gets two on each square! It saysthat each square has twice as many as the one before. It has to bemore than 128!" corrected Meredith.

react substantively to others' comments.

"We need to examine this situation in some organized fashion.I want you to get in your groups of four and determine the people whowill serve the usual roles of leader, recorder, reporter, and analyzerof group interaction," stated Mr. Santos.

use standard cooperative learning strategies.

One group decided to develop a computer program which printed atable listing the number of the square, the number of coins on thatsquare, and a subtotal to that point.

use technology to help solve the problem.

Another group borrowed the class chessboard and began placing playcoins on the squares. It soon became obvious to them that they wouldnot have enough play money to complete this attempt. They started tomake a table with the information they had constructed and worked tofind a pattern which they could extend to the complete board. Theirtable only included columns showing the number of the square, thenumber of coins on that square, and a column to list patterns. Theydiscovered that the number of coins could be represented by raising 2to the power which was one less than the number of the square. Usingcalculators, they found the number of coins on each square and thenthe total number of coins.

Another group began making a table similar to the group above, butthey also included a column showing the partial sums and another whichattempted to find a pattern in the partial sums. Eventually, theydiscovered that the partial sum at each square was one less than 2raised to the power equal to the number of the square. They couldthen quickly utilize the calculators to compute the total.

concretely model the problem before they move on to moresymbolic procedures.

use self-assessment to determine the effectiveness of theirmethod.

analyze mathematical situations by recognizing and usingpatterns and relationships.

At the end of the period, Mr. Santos reminded the groups that theywere to prepare a report of their methods which included a descriptionof their processes, an explanation of why they chose them, and theirevaluation of their processes. He asked each of them to consider themagnitude of their answer and find some way to explain to anotherperson just how large the answer was. Students brainstormedsome ideassuch as the distance between two known points or objects, themagnitude of the national debt, and the number of people on earth.

choose technology to reduce the computational load.

write about their approaches and solutions to problems.

connect their knowledge of mathematics to the realworld.

Ms. Ramirez announces to her seventh grade class that in threeweeks they will make a journey to Trenton, the capital of New Jersey.They will be visiting eight sites - the Capitol, the New JerseyMuseum, the War Memorial, the Old Graveyard, Trent House, the OldBarracks Museum, the Firehouse, and the Pedestrian Mall. To ensurethat they spend as much time at the sites as possible, and do aslittle walking as possible, the class must find the most efficientwalking tour for the trip, starting and ending at the parking lot.

The students:

apply mathematical skills to solve a real-world problem.

The first problem that the students must address is finding thewalking distance between each pair of sites. Ms. Ramirez supplieseach team with a street map and a ruler; the maps identify all thesites to be visited and the routes joining them. She assigns eachgroup the task of finding the distances between one site and all theothers. This turns out to be an interesting task, since differentgroups interpret it differently. Some groups, for example, measurethe straight line distance between two sites forgetting that buildingsor ponds might render that walk impossible. How to measure thewalking distance thus becomes an important topic of discussion, asdoes the question of appropriate units. These questions areeventually settled and the teacher uses the students' measurements towrite a matrix which indicates the walking distance between any two ofthe eight sites; different groups occassionally have obtaineddifferent numbers, but after discussion, they have arrived at a commonanswer.

use cooperative group work to generate problem-solvingstrategies.

freely exchange ideas and participate in discussions requiringhigher-order thinking.

collect and organize data needed to solve the problem.

Ms. Ramirez selects a sample route for the walking tour and throughdiscussion with the class explains how the total length of the walkingtour is obtained from the matrix of information that the studentsgenerated - you find the distances between consecutive sites onthe tour, and then add up the walking distances along the tour. Shenow asks her students to work in groups to decide on a strategy thatthey think will produce an efficient route (which starts and ends atthe parking lot), and to assist the group's recorder in writing ashort paragraph explaining their strategy. Some groups decide to listall possible routes and calculate how long a walk each route entails.(Ms. Ramirez asks the students how many possible routes do they thinkthey will have to list.) Other groups suggest that the best route isobtained by always going to the nearest site.

recognize there are numerous ways to solve the problem.

work in cooperative groups to develop alternativestrategies.

Ms. Ramirez now asks the students to use calculators to carry outtheir strategy and determine the travel time for the routes they willbe considering. After each group presents its results, the class willtogether compare the various methods that were proposed and theaccompanying results. Among the questions which Ms. Ramirez will askare: "Do the various methods give the same result?","Which methods result in a most efficient route?","What other strategies could we have used?" Responses fromthe students might include: "always use the shortestdistance", "never use the longest distance", "putdistances in increasing order and use only those that neither make aloop or put a third edge into a vertex."

compare the variety of strategies proposed.

As a regular feature in his class, Mr. Arbeiter has parents of eachstudent make a presentation about their job and how the variouseducational disciplines are needed for them to be successful. Today,Emily has asked her Mom, the owner of a heating and air conditioningcompany, to talk to her class. Mrs. Flinn and Mr. Arbeiter decide tohave the students help her solve a problem similar to one which hercompany faces regularly. She briefly describes her company, the workthat she does, and tells the students that they are going to help herdetermine how large an air conditioner will be needed in theclassroom. She poses the following problem: What information aboutthe room would be most important in determining how large an airconditioner is needed? The students quickly agree that the amount ofair conditioning would depend on the amount of air in the room, andthat in turn, depended on how much space there was in the room.Through suggestions and hints, Mrs. Flinn had them realize that theamount of sunlight entering the room would have an effect as well andthey quickly agreed that the area of the windows must be foundtoo.

The students:

interact with parents who use mathematics and other disciplinesin their daily lives.

have the time to explore a problem situation thoroughly.

Mr. Arbeiter reminded the class that there is a mathematical termwhich represents the amount of space, and asked each student to writedown that term. As was his custom, Mr. Arbeiter asked six students,one quarter of the class, to read the words they had each written.Four read the word "volume" and two read "area."By a show of hands, he found that about one third of the class hadwritten "area" and two thirds had written"volume." In their groups, the students were asked todiscuss the difference between area and volume and to write down thedifferences between them. As the groups discussed these conceptsMrs. Flinn and Mr. Arbeiter circulated among them, making sure thateach group had focused on the difference between area and volume;subsequently the groups read the statements they had prepared, and theentire class discussed and commented on the groups' statements.Mrs. Flinn had the class discuss which of the concepts were needed onthe two phases; amount of space in the classroom and how much windowspace there was.

are regularly assessed through a variety of methods.

work in a variety of settings to develop concepts andunderstanding.

Now that all students agreed on the difference between area andvolume and where each applied in this case, the discussion turned todiscussion centered on how one obtains the volume of the classroom andthe area of the windows. Although familiar with the concept ofvolume, the class was not able to calculate volume easily, soMr. Arbeiter suggested that each group build a rectanguar box out ofcubes and figure out how many cubes the box contained. Most groupsdiscovered that they could get the answer by multiplying the number ofcubes in the bottom layer by the number of layers (the"height"), and agreed with Mr. Arbeiter's conclusionthat V = BxH. When Mr. Arbeiter asked them how they calculate thenumber of cubes in the bottom layer, all agreed that you multipliedlength times width; and when the teacher wrote V=BxH=(LxW)xH, severalother groups recognized that that was how they found the volume oftheir box.

Mr. Arbeiter asked the class "How does the volume formula helpus find the volume of the classroom?" The students agreed thatthe shape of the classroom was about the shape of a rectangular box,but were quick to point out that to any answer obtained by the formulawould have to be considered an estimate, since it would not be takingalcoves and pillars into consideration. They agreed to change thequestion to "How does this formula help us estimate the volume ofthe classroom?"

use concrete materials to develop a model for volume.

"All we have to do is measure the three quantities -length, width, and height, the three dimensions of the classroom, andmultiply the three numbers together" was the prevailingsentiment. Marcia observed that "since we're only going to getan estimate anyway, why should we measure those three amountsexactly?" And Mrs. Flinn noted that her sales people oftenestimated the size of the room without making any measurements."How can we estimate the dimensions of a room withoutmakingmeasurements?", she asked. Paula suggested that"maybe the salesperson estimates the three dimensions andmultiplies those estimates together." "A greatsuggestion," Mrs. Flinn responded. "Let's try thatourselves."

recognize and apply estimating to geometric situations.

are exposed to a variety of open-ended questions and respond.

"Let's first estimate the width of the room. About howmany inches wide is this room?" Brian pointed out that inches isan appropriate unit for a piece of paper, but not for a room. After abrief discussion, Mrs. Flinn revised her question to "About howmany feet wide is this room?"

feel comfortable identifying errors.

The students wrote down their estimates and explanations of howthey arrived at them. After hearing all of the students estimates andreasons, the students were asked to return to their regular groups anddecide as groups what they thought the width of the room was."Well," said Mr. Arbeiter, "you all gave good reasonsfor your estimates, but now let's see whose estimate was closest.We'll measure the width of the classroom." Great cheers wereheard for the groups whose estimate was closest to the actualmeasurement. The same process was repeated for length, and width aswell as estimating the window area of the classroom. Mrs. Flinnpointed out that estimates were getting closer to the actualmeasurements each time they did it. She then showed the class aformula used to determine the number of BTUs needed for a room interms of the volume of the room and the area of the windows. The dataobtained by the class for the volume and window area was entered inthe formula, and a quick calculation gave the number of BTUs neededfor the classroom. Mrs. Flinn wrapped up her presentation by makingthe connection between the size needed, the cost of the purchase, andthe regular expense of running the air conditioner. She emphasizedthat the success of her business rested on the sales people and theirability to estimate the needs well.

communicate their answers and defend their thoughtprocesses.

examine the correctness of their results.

Mr. Arbeiter thanked Mrs. Flinn for her presentation and asked thestudents how they would like to practice the skills they had discussedtoday. Feeling confident, the students volunteered to estimate thedata for their other classrooms. Mr. Arbeiter agreed to display theresults, so long as the students agreed to leave off estimating whiletheir other classes were in session.

extend their skills through practice in similarproblems.

"It isn't fair!", Jasmine announced to her class oneMonday morning. "I used up $10 worth of quarters playing aboardwalk game over the weekend at the shore, and I only won once.And all I got for winning was a lousy stuffed animal!"

Ms. Buffon often told her class that mathematics was all aroundthem, and had encouraged them to see the world with the eyes of amathematician. So she wasn't surprised that Jasmine shared thisincident with the class.

"Please explain why you thought there was mathematicshere," Ms. Buffon asked Jasmine.

The students:

recognize the role that mathematics can play in explaining anddescribing the world around them.

"Well, first of all, I threw the quarters onto a platformwhich was covered with squares, you know, like a tile floor, so thatreminded me of geometry. And as I was throwing my quarters away, oneafter another, I was reminded of all the probability experiments thatwe did last year, you know, throwing coins and dice. It wasn'texactly the same, but it was like the same."

"Those were very good observations, Jasmine," saidMs. Buffon, "you recognized that the situation involved bothgeometry and probability, but you didn't tell the class what you hadto do to win the game."

connect previously learned mathematics to the currentsituation.

"Oh, you just had to throw the quarter so that it didn't touchany of the lines!" Ms. Buffon asked Jasmine to go to the boardto draw a picture, explaining to her that not everyone will visualizeeasily the game she was talking about.

use different forms of communication to define a problem andshare their insights.

Every other Monday, Ms. Buffon began her geometry class with asharing session. Sometimes the "mathematics situations"that the students shared did not lead to extended discussions, inwhich case Ms. Buffon continued with the lesson she had prepared. Butshe was prepared to use the entire period for the discussion, and evencarry it over into subsequent days, if the students got interested inthe topic.

are afforded the opportunity to fully explore and resolvemathematical problems.

"Why didn't you think the game was fair?" she askedJasmine. Jasmine repeated what she had said earlier, that she shouldhave won more often and that the prizes should have been better.Other students in the class were asked to respond to the question, andafter a lively interchange, they decided that for the game to bereally fair, you should get about $10 in prizes if you play $10 inquarters; but, considering that they were having fun playing the game,and considering that the people running the game should get a profit,they would be satisfied with about $5 in prizes. Jasmine listened tothe conversation intently, and chimed in at the end "That lousybear wasn't worth more than a dollar or two!"

Moving the discussion in another direction, Ms. Buffon said"Now that we understand that it is possible to explain'fairness' mathematically, let us investigate Jasmine's gameto see if it really was unfair. What do you think were Jasmine'schances of winning a prize?"

explore questions of fairness, geometry, andprobability.

This question evoked many responses from the class, and after somediscussion the class agreed with Rob's comment that it all depended onthe size of the squares. Jasmine did not know the actual size of thesquares, so the class agreed that they might as well try to figure outthe answer for different size squares. Dalia pointed out that thislooked like another example of a function, and Ms. Buffon commendedher for making this connection to other topics they had beendiscussing.

are encouraged to make connections to other topics withinmathematics.

Returning to her previous question, Ms. Buffon suggested that thestudents do some experiments at home to help determine the probabilityof winning a prize. Each pair of students was asked to draw a grid onposter board, throw a quarter onto the poster board 100 times, andrecord the number of times the quarter was entirely within the lines;to simplify the problem, quarters that landed off the grid were notcounted at all. Different students chose different size grids,ranging from 1.5" to 3.5", at quarter inch intervals.

After school, Ms. Buffon visited the Math Lab where she spent sometime trying to find materials related to this problem. When shelooked under "probability" in the indexes of variousmathematics education journals, she was led to several articlesdiscussing geometric probability, which she learned is a branch ofmathematics which addresses problems like Jasmine's game. With theseresources available to her, Ms. Buffon no longer feels that she has tohave all the answers, and can entertain discussions about mathematicaltopics with which she is unfamiliar. Tomorrow she will be able totell the class what she has learned!

model problems and conduct experiments to help them solveproblems.

The next day the students reported on their results, and Ms. Buffontabulated them in the following chart, and, at the same time, plottedtheir results on a graph:

"Do you see any patterns here?", Ms. Buffon asked theclass. They all agreed that, as expected, the larger the size of thesquares, the more frequently Jasmine would have won the game."What do you think the size of the squares were on the boardwalkgame?" Ms. Buffon asked next. Everyone agreed that the squareswere most likely smaller than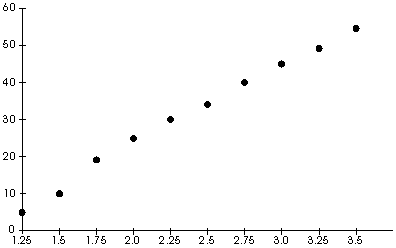

1.25" since her one prize out of forty quarters correspondedto 2.5 wins out of a 100 games, which was lower than obtained for thesmallest squares in the experiment. Turning to the graph,Ms. Buffonasked "What would have happened if we tried theexperiment with squares smaller than 1.25?" The studentslaughed, one after another, as they realized that if the size of thesquares were small enough, you would never win the game. "Well,then, what would have happened if we tried the experiment with largerand larger squares?" Looking at the graph, the class found thisa difficult question, but Fran broke the group's mindset by saying"Yeah, suppose the squares were as big as this room?" Theneveryone realized that if the squares were larger and larger, youwould become almost certain to win the game. "Dalia, do youremember your comment yesterday, that it sounded like we were workingon a function?" Ms. Buffon asked. "Would you sketch thegraph of that function for the class?" Ms. Buffon made a mentalnote to discuss this problem with her precalculus students, since shehad many questions to ask them about this graph.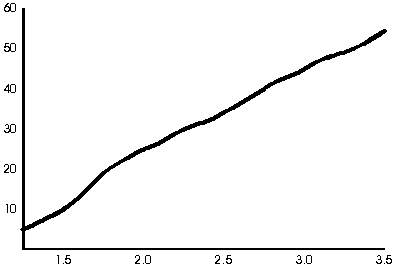

collect, analyze, and make inferences from data.

recognize connections between numerical patterns andfunctions.

"Well, we've gotten a lot of information by using experimentalmethods about Jasmine's game; let's see if we can figure out theprobability theory behind it as well." At this point, Ms. Buffonwas eager to tell her class what she had learned at the Math Lab.However, being aware that the students will grasp the solution methodbetter if they have an opportunity to discover it for themselves, sheasked the class to discuss the following question in their studygroups: "How can you tell from the position of the quarterwhether or not you would win the game?" Going from group togroup, Ms. Buffon listens to the discussions. When the groups havediscovered that to win the game, the center of the quarter must besufficiently far from the closest border, she gives the groups theirnext task - to describe where in the square the center of thequarter must be.

formulate and test mathematical conjectures.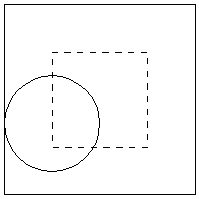

By reasoning in different ways, the groups all arrived at the samepicture involving a smaller square inside the original square, and atthe same conclusion - that you win if the center of the quarterlies inside the smaller square. With this information, the studentsare able to calculate the probability for any particular size of thesquare, and even to write an equation for the function whose graphthey sketched earlier.

Having found the probability of winning the game, Ms. Buffonplanned to return to the question that began this whole discussion- whether Jasmine's game was fair. But that was the topic foranother day.

Note: Ms. Buffon realized that the graph of the function was notlinear, as depicted earlier, even though the data seemed to indicatelinear growth. With her precalculus students, she would have themtranslate the above situation into the equationy=(x-d)²/x², where d is the diameter of thequarter. Then she would have them graph the function, enabling them todiscover that although the graph appears to be linear, in reality itincreases at a decreasing pace, and goes asymptotically to the line y= 1.

construct a pictorial model to represent the problem.

Ms. Jackson is teaching her geometry students to use and identifyinductive reasoning.

She asks each student to draw a large triangle on their paper. Shethen asks the students to hold up their triangles so that they can seethe wide variety that have been created. The students observe thatall the triangles are different.

Ms. Jackson then asks the students to cut out their triangle, totear off the corners of their triangle and to place the cornerstogether so that they are adjacent. She circulates around the room tobe sure everyone is on task, and tells students to record adescription of what they see in their notebooks.

The students:

use a variety of types of mathematical reasoning to solveproblems.

Ms. Jackson then asks a representative sampling of students to tellthe class what they observed after fitting the corners together. Thestudents report that it looks as if the corners form a straightline. Everyone agrees.

Ms. Jackson now asks the students to write a generalization aboutthe angles of ANY triangle based upon the class results of thisactivity. She asks another representative sampling of students tostate their generalizations. The students conclude that the sum ofthe measures of the angles of ANY triangle is 180 degrees.

She gives the students a definition of inductive reasoning. Theyrecognize that they have used induction to reach their generalizationabout the angles of a triangle. She then asks them to think aboutwhen they have used inductive reasoning in the past and write anexample in their notebooks.

are encouraged to form generalizations based on observationsthey have made.

Volunteers are asked to share their recollections with the rest ofthe class. Some are funny and some quite poignant. The teacher asksif anyone can see a drawback to inductive reasoning within social aswell as mathematical contexts.

The class decides that one drawback is that you can't check allexamples - all triangles cannot be checked to see if the angles alwaysadd to 180 degrees. Another is that if you check too few examples youmight reach an erroneous conclusion. They discuss how this is thereason for much of the racial and gender stereotyping that theyencounter. Ms. Jackson asks students to identify counterexamples forracial and gender stereotypes.

are regularly asked to write about their understandings ofmathematics and its uses in the real world.

Ms. Jackson then asks the students to do another experiment. Theyuse their compasses to draw 5 circles. On the first circle, thestudents identify and connect 2 points with a chord. They then statethe number of non-overlapping regions into which the circle has beendivided. On the second circle, students identify three points anddraw all chords connecting these points. Once again, they state thenumber of non-overlapping regions into which the circle has beendivided. They continue this procedure until they find the number ofnon-overlapping regions formed when 5 points on the circle are fullyconnected by chords. Students record their data in a table and useinductive reasoning to predict the number of non-overlapping regionsproduced by fully connecting n points on the circle with chords:

They are asked to state their conclusion in narrative form.

generate a set of data and use pattern-based thinking toformulate solutions.

The students agree that the number of non-overlapping regionsproduced by fully connecting n points on a circle with chords is2^(n-1). Students then test their conclusion by carryingout the experiment with 6 points. Many find their conclusion is wrongfor n=6. They fully expected to find 32 regions but only got 31!

As class draws to a close, Ms. Jackson gives a homework assignmentin which students will induce as well as produce counterexamples toconclusions. Students leave class somewhat dazed by the lastexperiment. Many of them tell Ms. Jackson that something must bewrong because they are sure the answer is 32. They tell her thatthey will prove her wrong by reenacting the experiment at home. Shelooks delighted and encourages their pursuit.

validate conclusions by looking forcounterexamples.

Mr. Miller wants his ninth grade mathematics class to review therectangular coordinate system, reinforce how mathematics is used tomodel situations, and develop the concept of exponential functions.He decides this would be an excellent opportunity to utilize areal-world situation. He elects to build his effort around anexperiment involving mold growth found in an old SMSG book entitledMathematics and Living Things.

At the beginning of the unit, Mr. Miller presents the class with apacket of required readings, each of which deals with growth patternsof living things. There is an article on the rabbit population ofAustralia, another on world population, and another on the spread ofAIDS. He explains the goals of the unit, gives the expectations forthe readings, and describes the purpose of the experiment the classwill conduct. Mr. Miller has students distribute the lab directionsand materials, and he has them prepare the medium for the moldgrowth.

The students:

incorporate scientific applications in their study ofmathematics.

On each day over the next two weeks, students record an estimate ofthe area covered by the mold, the increase in the area from theprevious day, and the percent of increase. On Fridays, they are askedto extrapolate the growth they expect to occur on Saturday and Sundayand then interpolate the same information from the growth they see onMonday. They are required to maintain a graph of the percent ofincrease versus the days. The extrapolated and interpolated pointsare both graphed with special marks such as "X" or"O."

estimate area of irregular figures.

collect and analyze data.

During the period of data-gathering, Mr. Miller develops

exponential growth through the concept of compound interest anduses a graphing calculator to illustrate the graph of such growth.Each student is asked to suggest a function which would yieldsomething close to their data, and has the opportunity to put theirfunction into the graphing calculator and revise it until they aresatisfied with the estimate. Time is provided to have the studentsdiscuss their reactions to the readings.

use technology as a tool of learning.

spend the time needed for mathematical discovery.

At the end of the two-week period, Mr. Miller has the studentsprepare a report relating the graph of their observations to thediscussions of the readings and the work on compound interest. Toextend the ideas developed in this experiment, students are givendifferent data sets which came from actualmeasurements of varioustypes of growth. Students work in groups, each group taking one ofthe sets of data. The groups are expected to make a presentationdiscussing the exponential function which models the growth, whatlimiting factors could be involved, and the carrying capacity of theenvironment.

write about their understandings of the connections betweenmathematics and physical phenomena.

extend their understanding of mathematical concepts throughcooperative work and presentation.

As a closing activity, students are asked to choose a country fromaround the world, examine population growth over some period of time,and write a paper for inclusion in their portfolio discussing themathematical issues and biological issues involved as well as ageneral discussion of the impact of such growth on the history of thatperiod.

are assessed through alternative means.

explore the uses of mathematics in other disciplines.