Thank you for visiting our site! You landed on this page because you entered a search term similar to this: second order differential equations solve, here's the result:
Second-order differential equations
Solution to the set of differential equations from the Lotka-Volterramodel for the Predator-Prey problem. In this example, the coyotes formthe predator population feeding on the rabbit prey. If the number ofrabbits increases, the number of coyotes eventually increases as well.Since the coyotes can, at some point, overwhelm the rabbits capacity toreproduce in a closed ecosystem, the number of rabbits eventually declines.At some point the number of coyotes that can be sustained by the rabbitsalso declines and the coyote population falls rapidly. When the numberof coyotes falls far enough, the rabbits start to reproduce enough toincrease their numbers and the cycle starts again. The solution to thedifferential equations in this case have to reflect the fact that thetrend to increase or decrease for either population depends on boththe number of animals in both populations and their tendencyto increase or decrease from those numbers. Thus the change in thepopulations for predator and prey form coupled differentialequations. The predator-prey problem forms one of the most popularexamples of such equations. Its study will reveal the difficulty ofvisualizing the solutions to such problems even in cases where a solutionis possible.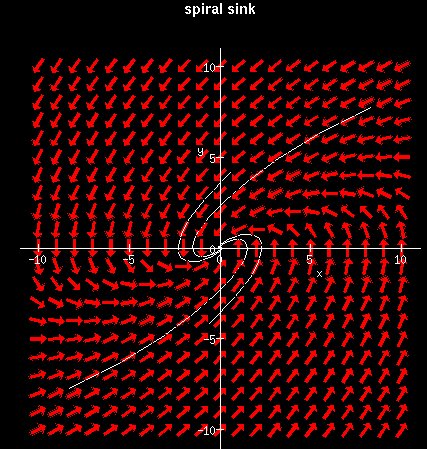
Depiction of solution to simultaneous equations for asink with rotational motion
Differential equations often arise in physics as consequences of Newton's second law:
(recall that the notation means ``take the derivative with respect to t. There is usually some physical description (often resulting in a mathematical model) of the force F -one that relates the force to the position of the moving particle (such as the distance of a massive particle from a gravitational source or of an electrically charged particle from another charged particle) or its velocity (think of air resistance as an example). The other side of the equation is purely mathematical, and if the mass of the particle is constant it involves the derivative of the particle's velocity - in other words, it involves the second derivative of the position of the particle. Thus, the mathematical problem that results from applying Newton's second law often takes the form of a differential equation for the position as a function of time. Since the differential equation involves second derivatives of the position, it is called a second-order differential equation.
If we take the example of a real spring, the motion we see is mimickedby the Java applet below:
Example: Undamped simple harmonic motion.
As a (highly idealized) example, consider the motion of a cart of massM attached to a nearby wall by means of a spring (see the figure). The spring exerts no force when the cart is at its equilibrium positionx = 0. If the cart is displaced by a distance x, then the spring exerts a restoring force proportional to the displacement and opposite in direction, i.e., F = -kx, where k is a positive constant whose magnitude is a measure of the stiffness of the spring (this expression for the force was postulated , and is sometimes called Hooke's law).
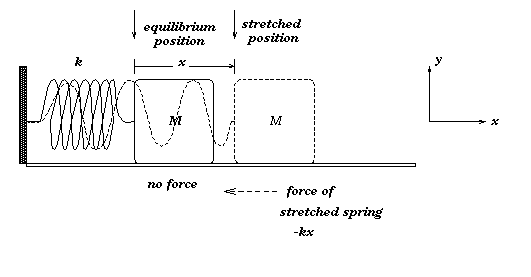
By Newton's second law, we have F = Mx´ ´ = -kx.We need a function whose second derivative is a negative multiple of itself. Exponential functions will not do in this situation,since the second derivative of is
, andr² must be positive if r is real.This provokes the idea of considering the exponentials of complex numbers (which we could do), or we could just look for another function.
If you ask Maple to dsolve the differential equation x´ ´ + x = 0, it will tell you that two possible answersare: x = sin t and x = cos t.(Verify this!) The relevant properties of the sine and cosine functions we need are: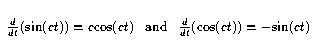 
Now we can use the stretch rule from the previous section to get that two possible solutions to are
and
.When you take a course in differential equations, you will learn that the most general solution of
is
for constants c_1 and c_2.
How are c_1 and c_2 determined?Often they are determined because we know some initial conditions, i.e., where the cart started and how fast it was going (just like in the falling object problems last week). For instance, suppose you know that
From the differential equation, we see that . Fromx(0) = 1, we see that c_2 = 1 (Why?). Then we have to computethe derivative:
Then we can use x´ (0) = 6 to get c_1 = 2. The solution of our initial-value problem is
Get more experience with dsolve by tackling exercise
Fri Mar 4 09:58:36 EST 1994subsection3_1_5.html