Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving non-linear differential equations simultaneous, here's the result:
Carrier Distribution and Screening
To understand how any heterostructure device operates, one must be able to visualize the energy-band profile of the device, which is simply a plot ofthe band-edge energies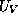 
and 
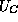as functions of the position x. These energies include the effects of the heterostructure energies 
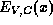and the electrostatic potential 
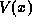. The electrostatic potential of coursedepends upon the distribution of charge within the device 
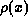. In general, 
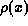depends upon the current flow within the device, and the evaluation of a self-consistent solution for the potential, carrier densitiesand current densities is the fundamental problem of device theory. However, in many cases, one may obtain an adequate estimate of the band profile byneglecting the current, and assuming that the device can be divided intodifferent regions, each of which is locally in thermal equilibrium with a Fermi level set by the voltage of the electrode to which that region is connected. We will refer to this as a quasi-equilibrium approximation. Such calculations are readily performed on computers of very modest capability. The formulation of the quasi-equilibrium problem of course holds exactly in the case of thermal equilibrium (no bias voltagesapplied to the device), and the equilibrium band profile of a heterojunctionhas been studied by Chatterjee and Marshak [41] and by Lundstrom and Schuelke [42].
It is fairly common for heterostructures to create regions in which the carrierdensities become quantum-mechanically degenerate. One therefore needs to takedegeneracy into account in evaluating the carrier densities. We will assume that the energy bands are parabolic, so that the quasi-equilibrium carrier densities are
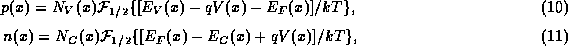
where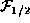 
is the Fermi-Dirac integral of order 
,
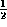and the effective densities of states are
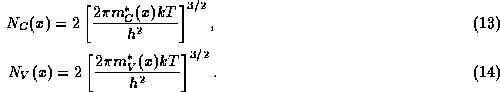
It is not particularly useful to express p and n in terms of the intrinsic density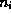
and the intrinsic Fermi level 
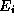, because these quantities are notconstant throughout a heterostructure. (Formulations which emphasize these quantitiesrequire the definition of an excessive number of auxiliary quantities to express the content of the heterostructure equations [42,43].) Also, the usefulness of 
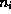in the elementary pn junction theory follows primarily from the mass-action law, 
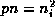, which is not valid in a degenerate semiconductor.
The net charge density includes contributions from the mobile carrier densities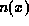 
and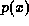 
, and from the ionized impurity densities 
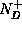and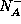 
. If one takes into account the impurity statistics, the ionized impurity densities will depend upon the potential:
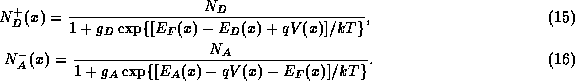
Here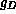 
and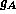 
are the degeneracy factors of the donors and acceptors,respectively, and the impurity state energies 
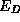and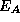 
are defined with respect to the same energy scale as 
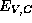. The total charge density is then
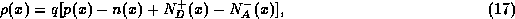
Note that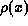 
depends upon 
, 
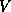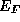, and the band parameters 
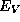and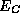 
through equations (1) and (1).
With the above expressions for the charge density, the electrostaticpotential is described by Poisson's equation, plus the appropriate boundary conditions. In a heterostructure, the dielectric constant will typically vary with semiconductor composition, so Poisson's equation must be written as
This form guarantees the continuity of the displacement. The screening equation fora heterostructure is obtained by combining all of the equations in thissection into (18). It is a nonlinear differential equation for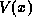 
, as the materials parameters are fixed by the design of the heterostructure, and the Fermi levels are fixed by the external circuit.The solutions to this nonlinear equation are well behaved and stable, however,because the charge density varies monotonically with 
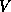and has the screening property: making the potential more positive makes the chargedensity more negative and vice versa.
The boundary conditions to be applied to this screening equation follow from the condition that each semiconductor material must be charge-neutral far from the heterojunction. Let the boundary points be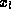 
and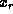 
.These can be taken to be 
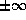if one is solving for the potentialanalytically, but if numerical techniques are used 
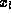and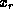 
should befinite but deep enough into the bulk semiconductor that charge neutralitymay be assumed. One then determines 
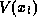and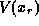 
simply bysolving
The physical picture that is assumed in this formulation is that the Fermi energy (possibly different in different regions of the device) isset by the voltages on the terminals of the device. The terminals, togetherwith the circuit node to which they are connected, are charge reservoirswhose chemical potential is just the Fermi level. The device and the circuit exchange charge, and the entire energy band structure, floats up or down until charge neutrality in the bulk is achieved. Thus the origin of the scale of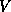 
is set by the combined choice of the energy scale for the band-structure energies 
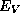and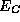 
, and the choice of ground potential for the circuit voltages (and thus the Fermi levels).The Fermi energies on each side of the junction 
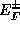are determined by the externally applied voltages at the respective contacts.In fact, it is most convenient to define the Fermi energy with respect to the circuit ground potential so that
where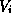 
is the voltage of the circuit node connected to the i'th device terminal.
If the carrier densities are neither degenerate nor closely compensated, the Fermi functions in (1) may be approximated by exponentials and one may directly solve for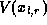 
to obtain the more familiar expressions:
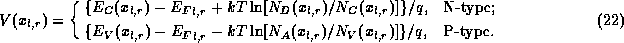
The diffusion voltage, which appears in the standard pn junction analysis, is justthe magnitude of the potential difference across the heterojunction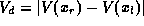
.
The screening equation consisting of Poisson's equation (18) combined with the charge density expression (17) and subject to the boundary values obtained by solving (1) is a nonlinear differential equation for the electrostatic potential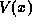 
.It is best solved numerically for each specific case, due to the large numberof band alignment topologies. An effective approach is to make a finite-difference approximation to the equation, reducing it to a set of simultaneous nonlinear algebraic equations, and solve these using Newton's method (see Selberherr [44]). The examples presented below were calculated using this approach.
If a given heterojunction is doped so as to achieve the same conductivity type on both sides of the junction (n-n or p-p), the junction is said to be isotype.If opposite conductivity types are achieved (p-n or n-p), it is an anisotypejunction. Figures 13--15 illustrate a few of the many possible band profiles that can be obtained with heterojunctions.
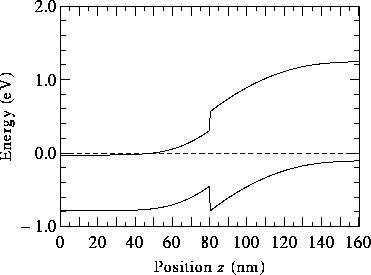
Figure 13: Self-consistent band profile of an anisotype straddling heterojunction in equilibrium. The In
Ga
As-InP heterojunction was chosen to emphasize the band discontinuities.
Figure 13 shows the band profile of an anisotype straddling junction in equilibrium. Apart from the band-edge discontinuities the profile resembles that of a pn homojunction.
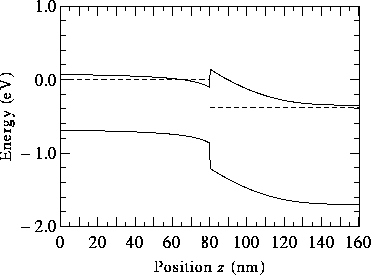
Figure 14: Self-consistent band profile of an isotype heterojunction under a small reverse bias. Again the In
Ga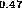
As-InP is shown.
An isotype junction is shown in Fig. 14. Its band profile resembles that of a Schottky barrier. Figure 15shows the profile of a broken-gap system. The bands are fairly flat, despite the fact that this is an anisotype junction.
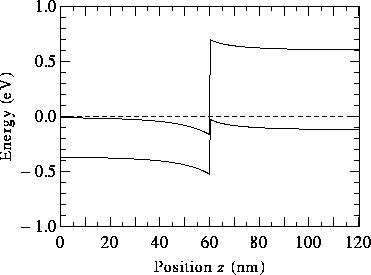
Figure 15: Self-consistent band profile of a broken-gap (N)InAs-(P)GaSb heterojunction in equilibrium. This doping configuration is the most easily fabricated.
William R. Frensley
Sun May 21 16:29:20 CDT 1995