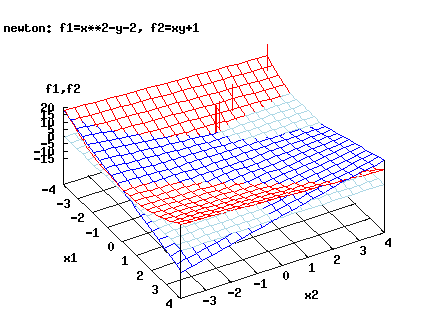
The following table shows performance of Newtons method for the problem f1=x**2-y-2=0 and f2=x*y+1=0 with initial guess -4,4
See also the picture. The solutions of the system occurwhere the three colors corresponding to the surfaces z=f1(x,y), z=f2(x,y) and z=0(red , dark blue and light blue) meet. The iterates are represented by vertical bars.
 | | f is a function of one real variable (Brent-Decker method), using function values only, zerofinder , needs inclusion by change of sign on interval |
 | SERVER | server routines for brent.shar (C) |
 | DFZERO | SLATEC root finder Java version |
 | polyzero | f is a polynomial of one complex variable and has real coefficients (least squares method, interactive/file input, f77/C) |
 | MultRoot
| f polynomial with real (inexact) coefficients, especially for multiple roots (Matlab) |
 | companion
C-version | f polynomial with real coefficients, QR for eigenvalues of companion matrix |
 | Aberth
C-version | f is a polynomial with complex coefficients |
 | Muller
C-version | f is a general function of one complex variable |
 | ZERO | search for a zero in a given interval |
 | RPOLY | find all zeroes of a real polynomial(Jenkins-Traub method)f90-version |
 | Madsen | find all zeroes of a real polynomial, C++ version |
 | CPOLY | find all zeroes of a complex polynomial(Jenkins-Traub method) | find all zeroes of a complex polynomial(several methods, root refinement, Windows version) |
 | RROOT | safely enclosing zeroes of a continuous function in an interval |
 | KINSOL | part of the SUNDIALS suite for ODE/DAE (C, Fortran interface) |
 | ALIAS | Solve systems of equations or inequalities with interval arithmetic (C++) |
 | box_zeros | f depends on one or more complex variables, zeros sought in box (based on TOMS666) |
 | HYBRJ | f not too nonlinear, exact Jacobian (Powell's hybrid method) |
 | HYBRD
f90 version | not too nonlinear, Powells hybrid method, finite difference Jacobian |
 | DogLeg | Powell's dogleg method (Matlab) |
 | csolve | Robust solver by C. Sims (Matlab) |
 | BROYDEN-MEX | Matlab interface to quasi-Newton Fortran code |
 | STRSCNE | Trust region method for bound-constrained nonlinear systems (Matlab) |
 | CRBond's code | real/complex one/multidimensional rootfinders and LS solvers (C/C++) |
 | Filtrane | part of Galahad, nonlinear constraint solver, filter method, f90 |
 | PITCON | f not too nonlinear, no good initial guess available, continuation method |
 | ALCON1 | Continuation method for systems of algebraic equations f(x,tau)=0. Optional computation of turning and (simple) bifurcation points (by Deuflhard and Kunkel) |
 | ALCON2 | Continuation method for systems of algebraic equations f(x,tau)=0. Optional computation of turning and (simple) bifurcation points (by Deulfhard, Fiedler and Kunkel). Optional automatic construction of completebifurcation diagrams. |
 | ALCON_S | Continuation method for systems of algebraic equations f(x,tau)=0. Large and sparse systems. (from elib/codelib, author Klein-Robbenhaar) |
 | LOCA | Library of continuation algorithms; uses bordering algorithm to permit very large dimensions; distributed memory parallel (C) |
 | Continuation Toolbox | Includes continuation of limit cycles and codim 1 bifurcations (Matlab) |
 | MATDS | Another Matlab continuation toolbox (for dynamical systems) |
 | nleq1 | f strongly nonlinear, damped Newtons methodMatlab version |
 | nleq1s | damped Newtons method, large and sparse problems, direct linear algebra |
 | nleq2 | damped Newtons method, provision for singular Jacobian |
 | NLEQ-paper | PDF file on above nleq* codes |
 | SNES | part of PETSC, serial and MPI parallel versions |
 | PEQN/PEQL | inexact Newton and inverse column update methods, for large/sparse problems |
 | giant | damped Newtons method, large and sparse problems, iterative linear algebra |
 | nnes | zeros sought in box: l,see also users' guide |
 | DAFNE | differential equations approach with second order system inspired by mechanics |
 | CHABIS | characteristic bisection method |
 | EPSILON | Maple-based package for operations on polynomials including solving systems |
 | HOMPACK | globally convergent continuation method for polynomial systems |
 | HOMPACK90 | f90 version of HOMPACK |
 | POLSYS_PLP | more sophisticated version of HOMPACK90 |
 | PHoM | Polyhedral Homotopy Continuation Method for Polynomial Systems (C++), module CMPS also in Matlab |
 | TENSOLVE | A Software Package for Solving Systems of Nonlinear Equations and Nonlinear Least-squares Problems Using Tensor Methods | A general-purpose solver for polynomial systems by homotopy continuation |
 | INTOPT_90 | f90, see under Interval software |