Problema Solution
The height (in feet) of the water level in a reservoir over a 1-year period is modeled by the function
H(t) = 3.3(t − 4)2 + 11
where t = 1 represents January, t = 2 represents February, and so on. How low did the water level get that year?
Answer provided by our tutors
We need to find the minimum of the function:
H(t) = 3.3(t − 4)^2 + 11
From the graph of the function we see that it has minimum:
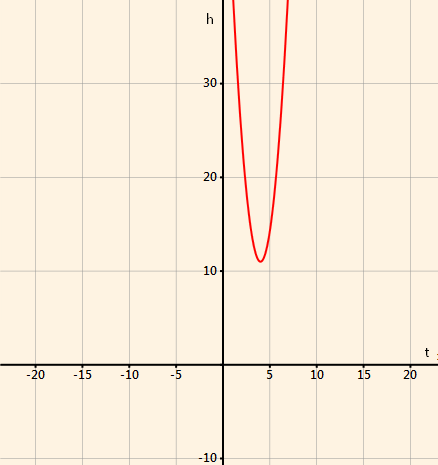
Now we will find the minimum.
By simplifying the function H(t) = 3.3(t − 4)^2 + 11 we get:
H(t) = 3.3t^2 − 26.4t + 63.8
The function is parabolic and has minimum:
H min = c - (b^2)/(4a), where a = 3.3, b = -26.4, c = 63.8
H min = 63.8 - ((-26.4)^2)/(4*3.3))
H min = 11 ft
The lowest water level that year was 11 ft.