ANSWERS FOR MATH PROBLEM SET VII
Section 14B, page 301.
15. Following the Euclidean algorithm, we find the following instances of the
division theorem in
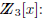
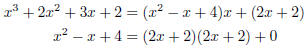
Thus one gcd is 2x + 2. The monic gcd is x + 1.
Now that we know the answer, let's look at the problem again. We are working
over 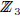 . The two
. The two
given polynomials can be factored :
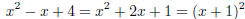 and
and
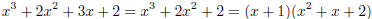
and x2 + x + 2 is irreducible in 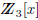 . From this
factorization, it is clear that the gcd is x + 1.
. From this
factorization, it is clear that the gcd is x + 1.
19. First, following the Euclidean algorithm, the have the following (obvious)
instances of the
division theorem :
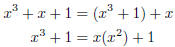
Thus we see that the gcd is indeed 1, so solutions exist .
Secondly, we can unwind this to obtain the Bezout polynomials.
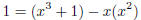 and
and
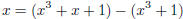
which together give
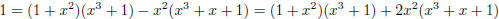
which is an equation in the desired form.
Section 14C, page 305.
38. We are given that q = pr for some r. Since q is irreducible and p is not a
unit, we conclude
that r is a unit. Both p and q are monic, so r = 1.
42. Having read the hint, we observe that
 . So the two
given polynomials
. So the two
given polynomials
are
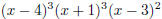 and
and
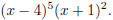
The gcd is 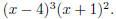
45. Counterexample: In the field of polynomials over the reals, let
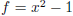 ,
with n = 2. Then
,
with n = 2. Then
f is reducible , but it has no irreducible factor of degree < 1/1.
The author must have meant "< n/2" to be " ≤n/2." Now the result is pretty clear .
We have
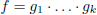 where k≥2, the gi's are irreducible,
and
where k≥2, the gi's are irreducible,
and 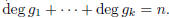 So we could not have
So we could not have
both 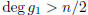 and
and
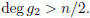 That is, either
That is, either
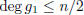 or
or 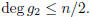
46. In 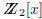 , there are of course two linear polynomials (i.e., degree 1), four
quadratic polynomials
, there are of course two linear polynomials (i.e., degree 1), four
quadratic polynomials
(degree 2), eight cubic polynomials (degree 3), and sixteen quartic polynomials
(degree 4).
We know that both the linear polynomials , x and x + 1, are irreducible. For the
quadratics and the
cubics, any polynomial with a root in 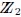 is reducible, because it will have a
linear factor, by the root
is reducible, because it will have a
linear factor, by the root
theorem. And if it does not have a root, then it will be irreducible, because
for 2 or 3 to be the sum of
two smaller numbers, one of those smaller numbers must be 1.
In this way, we find one quadratic , 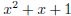 , and two cubics,
, and two cubics,
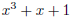 and
and 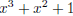 , that are
, that are
irreducible.
For the quartics, there are four without roots. But might they be the product of
irreducible quadrat-
ics? Because there is only one irreducible quadratic, this consideration
eliminates only one quartic, its
square . The other three are irreducible: 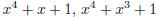 , and
, and
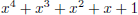 .
.
That finishes the problem. Nonetheless, we add here a list of all 32 polynomials
in![]() with degree
with degree
4 or less, with their factorization into irreducible polynomials.
| 0 | zero | 1 | unit | |
| x | irreducible | x + 1 | irreducible | |
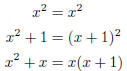
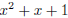 irreducible
irreducible
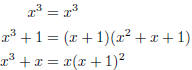
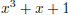 irreducible
irreducible
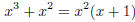
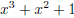 irreducible
irreducible
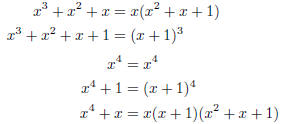
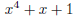 irreducible
irreducible
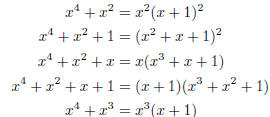
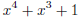 irreducible
irreducible
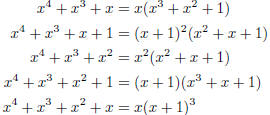
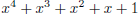 irreducible
irreducible
Section 15D, page 319.
18. We are given the valuable clue that 3+2i is a root of f. Therefore 3-2i is
also a root, and f
is divisible by the quadratic

When we carry out the division, we obtain
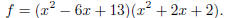
Because x2 + 2x + 2 has no real roots, it is irreducible over the reals, and we
are done.
21. We seek a multiple of f that has real coefficients. Following the hint, we
calculate
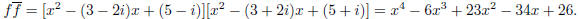
| Prev | Next |