The Quadratic Formula
Introduction
The following worksheet illustrates the use of a quadratic
equation solution for showing the effect of
significant digits on round-off errors The user will enter the a, b and c values
as given by the equation
for the standard form of a quadratic equation : ax^2 + bx + c = 0, as well as the
number of significant
digits to be displayed in a table that will be created at the end of the
program. Two variations of the
quadratic equation solution will be used :
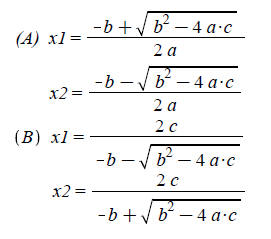
Initialization
restart : with Statistics :
Section 1: Input
This is the only section where the user interacts with the
program.
The quadratic formula is derived from the standard form of a quadratic equation:
ax^2 + bx + c = 0
Enter coefficient a
| a := 0.001 | |
|
a := 0.001 |
(3.1) |
Enter coefficient b
| b :=-4.94627 | |
|
b :=-4.94627 |
(3.2) |
Enter coefficient c
| c := 0.002 | |
|
c := 0.002 |
(3.3) |
Enter range of significant digits to be used.
| sig_low := 7 sig_high := 10 |
|
|
sig_low := 7 |
(3.4) |
This is the end of the user section. All
information must be entered before proceeding to the next
section. RE-EXECUTE THE PROGRAM.
Section 2: Simulation
The following calculations will be performed inside a loop
so that the number of significant digits
used can be varied as specified by the user. The digits command will be used to
control the number
of digits Maple uses when calculating.
Variation 1:
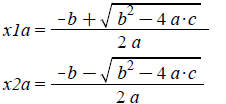
j :=sig_low :
for i from sig_low to sig_high do
Digits :=i;
x1a[j] :=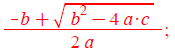
x2a[j] := evalf 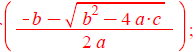
j :=j+1;
end do:
Variation 2:
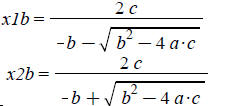
j :=sig_low :
for i from sig_low to sig_high do
Digits :=i;
x1b[j] :=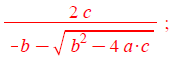
x2b[j] :=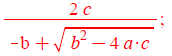
end do:
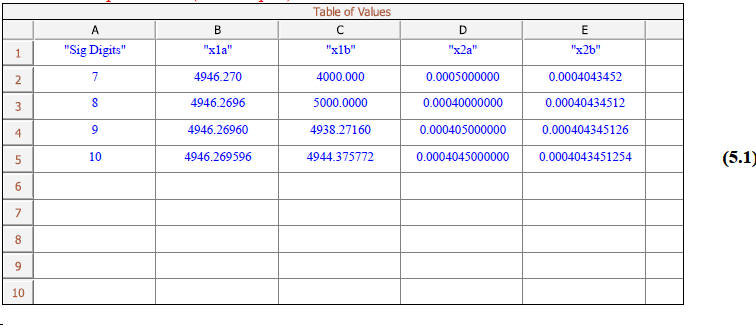
Section 3: Spreadsheet
This table shows the values of x1a, x2a, x1b, and x2b and
the number of significant digits used in
their calculation.
n :=1 :
with Spread :
tableoutput :=CreateSpreadsheet "Table of Values" :
SetCellFormula (tableoutput, 1, 1, "Sig Digits") ;
SetCellFormula (tableoutput, 1, 2, "x1a" ;)
SetCellFormula (tableoutput, 1, 3, "x1b" ;)
SetCellFormula (tableoutput, 1, 4, "x2a" ;)
SetCellFormula (tableoutput, 1, 5, "x2b" ;)
for j from sig_low to sig_high do
SetCellFormula (tableoutput, nC1, 1, j );
SetCellFormula (tableoutput, nC1, 2, x1a[j]);
SetCellFormula (tableoutput, nC1, 3, x1b[j]);
SetCellFormula (tableoutput, nC1, 4, x2a[j]);
SetCellFormula (tableoutput, nC1, 5, x2b[j]);
n :=n+1;
end do:
EvaluateSpreadsheet (tableoutput)
Section 4: Graphs
These bar graphs show the values of x1 and x2 for both variations of the quadratic function.
Data1 :=Array ([seq (x1a [i] , i = sig_low ..sig_high)])
:
Data2 :=Array ([seq (x1b [i] , i = sig_low ..sig_high )]):
ColumnGraph ([Data1, Data2] , offset = sig_low, title
= " Value of First Root as a Function of Significant Digits", legend = ["x1a",
"x1b" ],
titlefont = [ TIMES , BOLD, 12] , labelfont = [TIMES, ROMAN, 12 ], labels
= ["Number of Significant Digits", "Value of Quadratic Root"] , legendstyle =
[location
= right];
Data3 :=Array ([seq x2a [i] , i = sig_low ..sig_high )]):
Data4 :=Array ([seq x2b [i] , i = sig_low ..sig_high )]):
ColumnGraph ([Data3, Data4] , offset = sig_low, title
= "Value of Second Root as a Function of Significant Digits", legend = ["x2a",
"x2b" ],
titlefont = [ TIMES , BOLD, 12] , labelfont = [TIMES, ROMAN, 12] , labels
= ["Number of Significant Digits", "Value of Quadratic Root"] , legendstyle =
[location
= right ]);
Value of First Root as a Function of Significant Digits
| Value of Quadratic Root | 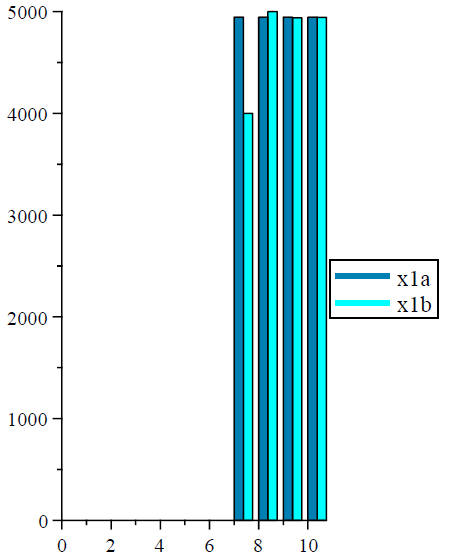 Number of Significant Digits |
Value of Second Root as a Function of Significant Digits
| Value of Quadratic Root | 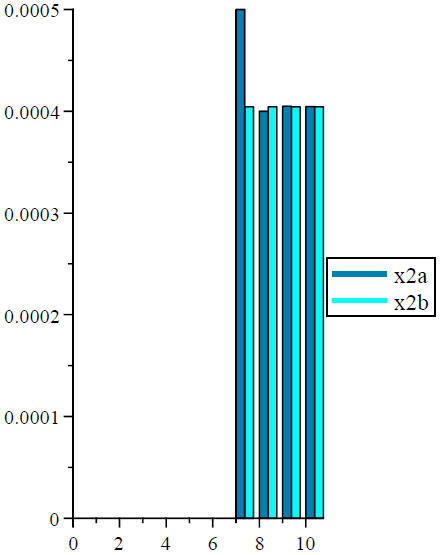 Number of Significant Digit |
Conclusion
Subtraction of numbers that are nearly equal can result in
unwanted inaccuracies. The number of
significant digits used in calculations plays a large role in the creation of
these inaccuracies and the
magnitude of the round-off errors. Hence, when the accuracy of calculations is
critical, it is
necessary to understand possible sources of error and how they are best avoided.
Legal Notice: The copyright for this application is
owned by the author(s). Neither Maplesoft nor the
author(s) are responsible for any errors contained within and are not liable for
any damages resulting
from the use of this material. This application is intended for non-commercial,
non-profit use only.
Contact the author for permission if you wish to use this application in
for-profit activities.
| Prev | Next |