Basic College Algebra

	Learning Objectives
L1 Real Numbers and Algebra Review (R.1, R.2) Due date: 01/12
	1. Classify the numbers. Identify the sets of natural, integer, rational, irrational, and real numbers. Perform operations on the set of real numbers. Work with properties of real numbers. Evaluate numerical expressions using the order of operations. 2. Compute absolute value of a number or expression. Find the distance between two numbers on the number line. 3. State laws of exponents. Simplify expressions by using the laws of exponents. 4. Define the square roots. Evaluate the principal square root. Convert between scientific and decimal notation. Perform operations in scientific and decimal notations.
L2 Polynomials; Factoring Polynomials (R.4, R.5) Due date: 01/12
	Learning Objectives
	5. Recognize monomials. Recognize polynomials. 6. Perform operations of addition, subtraction, and multiplication on polynomials. Use the special product formulas for polynomial expansion and factoring. 7. Factor out the common factor. Factor polynomials by grouping. Define prime (irreducible) polynomials. Factor polynomials over the various sets of numbers: integer, rational or real numbers. 8. Factor quadratic trinomials by using FOIL “in reverse”. Use method of substitution for factoring polynomials.
L3 Polynomial Division; Synthetic Division; Rational Expressions (R.4, R.6, R.7) Due date: 01/15
	Learning Objectives
	9. Divide polynomials by using long division. Perform synthetic division where it is appropriate. 10. Define a rational expression and its domain. Reduce a rational expression to lowest terms . 11. Multiply, divide, add, and subtract rational expressions. Use the least common multiple method for adding or subtracting rational expressions. 12. Simplify complex rational expressions (complex fractions).
L4 nth Roots; Rational Exponents (R.8) Due date: 01/20
	Learning Objectives
	13. Define the principle nth root of a real number. Evaluate radical expressions. 14. Simplify radicals. Rationalize the denominators . Add and subtract radical expressions . 15. Define rational exponents. Simplify expressions with radicals and/or rational exponents.
L5 Linear Equations and Applications (1.1, 1.7) Due date: 01/22
	Learning Objectives
	16. Give the definition of an equation in one variable and its solution set. Describe the operations which, when performed on an equation, lead to an equivalent equation. 17. Solve linear equations and the equations that lead to linear equations. Solve an equation for the indicated variable. 18. Describe the steps for solving applied problems. Use mathematical modeling to solve applied problems on uniform motion, interest, mixture, constant rate job, and other applications.
L6 Quadratic Equations and Applications (1.2, 1.7) Due date: 01/26
	Learning Objectives
	19. Solve quadratic equations by factoring, using the square root method, completing the square. 20. Solve quadratic equations by using the quadratic formula. Use the discriminant to classify the types of solutions of a quadratic equation. Use the quadratic formula for factoring. 21. Solve applied problems involving quadratic equations.
L7 Complex Numbers; Quadratic Equations in the Complex Number System (1.3) Due date: 01/29
	Learning Objectives
	22. Define the complex numbers. Equate, add, subtract, multiply, and divide complex numbers. Simplify powers of i. 23. Define the principal square root of a negative number . Simplify expressions involving roots of negative numbers. 24. Use the quadratic formula for the equations with a negative discriminant. Solve quadratic equations in the complex number system. 25. Solve the equations that lead to the quadratic equations.
L8 Radical Equations; Equations Quadratic in Form; Factorable Equations; Equations Involving Absolute Value (1.3, 1.4, 1.6) Due date: 02/05
	Learning Objectives
	26. Discuss the steps in solving equations with radical and rational exponents. Be aware of possible existence of extraneous solutions. Solve the equations with radicals and rational exponents. 27. Identify and solve the equations quadratic in form. Solve biquadratic equations. 28. Solve factorable equations in the complex number system. 29. Recall the definition of the absolute value. Solve the equations involving absolute value.
L9 Solving Inequalities; Inequalities Involving Absolute Value (1.5, 1.6) Due date: 02/09
	Learning Objectives
	30. Use interval notation. Graph intervals. 31. State properties of inequalities. Use these properties to solve linear inequalities and inequalities that lead to the linear inequalities. Solve combined inequalities . 32. Solve inequalities involving absolute value. 33. Solve applied problems involving inequalities.
L10 Rectangular Coordinates; Graphs of Equations (2.1, 2.2) Due date: 02/12
	Learning Objectives
	34. Plot points in the rectangular coordinate system. Compute the distance between two points in the coordinate plane. Find the coordinates of the midpoint of a line segment. 35. Define an equation in two variables and its graph. Graph some basic equations by plotting points. 36. Find the intercepts of the graph of an equation. 37. Define the types of symmetry with respect to the x‐axis, the y‐ axis, and the origin. Test an equation for symmetry
L11 Circles; Lines (2.4, 2.3) Due date: 02/16
	Learning Objectives
	38. Write equations of a circle in various forms. Find the center and radius of a circle from the given equation. Graph a circle. 39. Define and interpret the slope of a nonvertical line. Find the slope of a nonvertical line. Graph lines given the point and the slope. Consider vertical lines for which the slope is undefined. Analyze the graph of a line using the slope. Graph a line. 40. Consider the various forms of the equations of lines such as the point‐slope, slope‐intercept, and general forms.
L12 Parallel and Perpendicular Lines; Relations; Functions (2.3, 3.1) Due date: 02/19
	Learning Objectives
	41. Give criteria for parallel and perpendicular lines. Find equations of parallel and perpendicular lines. 42. Give the definition of a relation. Distinguish functions from general relations. Determine whether a relation represents a function. 43. Find values of a function. Simplify the difference quotient. Define the domain and range of a function. 44. Perform the operations of addition, subtraction, multiplication, and division on two functions. Find the domain of the sum, difference, product or quotient of two functions.
L13 Graph of a Function; Properties of Functions; Library of Functions; Piecewise‐defined Functions (3.2, 3.3, 3.4) Due date: 02/23
	Learning Objectives
	45. Identify the graph of a function. Obtain information from or about the graph of a function. 46. Determine even and odd functions. Identify even and odd functions from the equation. 47. Use the graph to determine the intervals on which a function is increasing, decreasing or constant. Describe local maxima and minima. Use the graph to locate local maxima and minima. 48. Find the average rate of change of a function. Relate the average rate of change to the slope of the secant line. 49. Graph the functions listed in the Library of Functions. Graph piecewise‐defined functions.
L14 Graphing Techniques: Transformations; Mathematical Models (3.5, 3.6) Due date: 02/26
	Learning Objectives
	50. Graph functions using vertical and horizontal shifts. Graph functions using compressions and stretches. Graph functions using reflections about the x‐axis and the y‐axis. 51. Consider mathematical models of real‐world problems: build and analyze functions. Work with direct, inverse, joint, and combined variations.
L14a Linear Functions and Models; Quadratic Functions and Models (4.1, 4.2, 4.3, 4.4) Due date: 03/02
	Learning Objectives
	52. Define linear functions. Graph linear functions. Use the average rate of change to identify linear functions. Determine whether a linear function is increasing, decreasing or constant. 53. Consider models involving linear functions. Build linear functions from data: draw and interpret scatter diagram, distinguish between linear and nonlinear relations, use a graphing utility to find the line of best fit. 54. Graph a quadratic function by using transformations. Identify the vertex and the axis of symmetry of a quadratic function. Graph a quadratic function using its vertex, axis, and intercepts. 55. Find the maximum and minimum values of quadratic functions. Solve applied problems involving quadratic functions. Use a graphing utility to find the quadratic function of best fit.
L15 Polynomial Functions; Polynomial Inequalities (5.1, 5.4) Due date: 03/16
	Learning Objectives
	56. Identify a polynomial function and its degree. Investigate the properties and the end behavior of a power function. Graph polynomial functions using transformations. 57. Identify zeros of a polynomial function and their multiplicities. Analyze the behavior near a real zero. Define the turning points. Relate the number of turning points of a polynomial to its degree. 58. Analyze the end behavior of a polynomial function. 59. Graph polynomial functions. Find an equation of a polynomial function if the graph is given. 60. Analyze the graph of a polynomial function. Use a graphing utility to analyze the graph of a polynomial function. 61. Solve polynomial inequalities.
L16 Rational Functions (5.2) Due date: 03/19
	Learning Objectives
	62. Identify a rational function and find its domain. Define the real zeros of a rational function. 63. Define vertical asymptotes and holes of a rational function. Find the vertical asymptotes and the holes, if any. 64. Define horizontal and oblique asymptotes of a rational function. Find the horizontal or oblique asymptote of a rational function.
L17 Analyzing Graphs of Rational Functions; Rational Inequalities (5.3, 5.4) Due date: 03/23
	Learning Objectives
	65. Graph rational functions. Construct a rational function from the graph. 66. Solve applied problems involving rational functions. 67. Solve rational inequalities.
L18 Systems of Linear Equations: Substitution and Elimination; Systems of Nonlinear Equations (8.1, 8.6) Due date: 03/26
	Learning Objectives
	68. Identify systems of two equations in two variables. Define the solution set of the system of equations and discuss its geometrical meaning. Discuss the possible solution sets of the system of two linear equations in two variables. 69. Solve systems of two linear equations in two variables by substitution and elimination. 70. Solve applied problems by using systems of two linear equations in two variables. 71. Solve systems of nonlinear equations by substitution or elimination. Graph the equations of the system and locate the system’s solutions. Solve applied problems by using systems of two nonlinear equations in two variables.
L19 Zeros of a Polynomial Function; Fundamental Theorem of Algebra (5.5, 5.6) Due date: 03/30
	Learning Objectives
	72. State the division algorithm for polynomials. Use the Remainder and Factor Theorems. 73. State the Fundamental Theorem of Algebra. Prove the Number of Zeros Theorem. Factor polynomials by using its zeros. State the Conjugate Pairs Theorem. 74. Find all zeros of a polynomial function when one zero is given. Find a polynomial with specified zeros. 75. Use the Theorem for Bounds on Zeros. (Omit Descartes’ Rule of Signs , Rational Zeros Theorem). Use the Intermediate Value Theorem.
L20 Composite Functions; One‐to‐one Functions (6.1, 6.2) Due date: 04/02
	Learning Objectives
	76. Define a composite function. Compute values of composite functions. Find the expression for a composite function and its domain. 77. Find the components of a composite function. Consider applications involving compositions of two functions. 78. Introduce the inverse relation. Discuss when the inverse relation of a function is a function and relate it to the one‐to‐one functions. 79. Determine whether a function is one‐to‐one.
L21 Inverse Functions (6.2) Due date: 04/06
	Learning Objectives
	80. Define the inverse of a given function. Determine whether two functions are inverses of each other. 81. Apply the cancellation rules for the inverse functions. State the relation between the domain and range of the function and its inverse. Obtain the graph of the inverse function from the graph of a function. 82. Find the inverse of a one‐to‐one function which is defined by an equation. Find the inverse of a domain‐restricted function.
L22 Exponential Functions (6.3) Due date: 04/09
	Learning Objectives
	83. Define the exponential function. Compare exponential and linear models. 84. Graph exponential functions. Analyze the properties of exponential functions. 85. Solve exponential equations using the one‐to‐one property of the exponential function. 86. Define number e. Graph the exponential function with the base e.
L23 Logarithmic Functions; Applications of Logarithms (6.4) Due date: 04/13
	Learning Objectives
	87. Define the logarithmic function. State the cancellation rules for logarithms and exponents. Convert between logarithmic and exponential expressions. Solve logarithmic and exponential equations by converting from one form to another. 88. Graph the logarithmic function. Analyze the properties of the logarithmic function knowing the properties of the exponential function. 89. Give a definition of 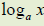. Evaluate logarithms with and without a calculator. 90. Define the natural logarithmic function. Graph natural logarithmic functions. 91. Consider applications of logarithms.
L24 Properties of Logarithms; Logarithmic and Exponential Equations (6.5, 6.6) Due date: 04/20
	Learning Objectives
	92. State the properties of logarithms. Simplify expressions by using the properties of logarithms. Use the change‐of‐base formula. 93. Solve logarithmic equations. 94. Solve exponential equations.
L25 Applications of Exponential Function; Logistic Models; Building Models from Data (6.7, 6.8, 6.9) Due date: 04/22
	Learning Objectives
	95. State the compound interest formula. Consider continuous compounding. 96. Determine the present and the future value of a lump sum of money. 97. Determine the rate of interest and time required to obtain a certain amount of money. 98. Find equations describing the quantities that obey the law of uninhibited growth and decay. Find the half‐life of a radioactive substance. 99. Use logistic models. 100. Use a graphing utility to fit exponential, logarithmic, and logistic functions to data
L26 Mathematical Induction; the Binomial Theorem (9.4, 9.5) For extra credit. Due date: 04/22
	Learning Objectives
	101. Prove statements using method of mathematical induction. 102. Evaluate 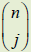. 103. State the Binomial Theorem. Expand binomials. Evaluate a specified coefficient in a binomial expansion. 104. Describe the Pascal’s triangle. Use the Pascal’s triangle to write the binomial expansions which relate to small natural numbers n.