Numerical Methods

Topics:
Numerical Methods Introduction
WHY ARE WE STUDYING THIS???
matrix methods
curve fitting
root finding
optimization
statistical analysis
probability analysis
integration / differentiation
ordinary differential equations
signal processing

NUMERICAL METHODS (why?)

Our creations are based on mathematical models of what occurs in nature.

• Structural response to wind/waves/earthquakes
• Airplane performance
• Chemical reactions
• Automobile suspensions
• Steel bridge deformation under heavy railroad loads
• Traffic patterns for infrastructure design
• Maximum capacity of piles holding up foundations
• Waste water treatment plants
• The betting line on Florida vs. Florida State
• Insurance premiums
• ......

These mathematical models of physical processes allow us to design and build new creations that account
for the various stresses they will see. Without numerical methods (the creation and application of
mathematical models), there would be no aircraft, tall buildings, long bridges, etc.

We’ll look at a brief introduction of each of the topics to be covered.

Matrix methods - solving simultaneous equations

• We’re familiar with the equation relating force and displacement for a spring as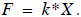
• We’ve also learned how to analyze a simple truss structure in statics
• All a truss is permitted to do is stretch or compress. So one way of analyzing truss type structures is to
visualize the structure as a group of attached springs. For example, the simple truss below can be represented
as springs.

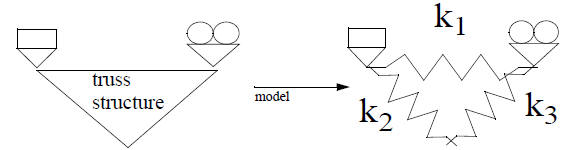
• Usually engineers know what the constant k is for each spring, and the forces F acting on the structure.
• If a force pushes or pulls on the end of one spring, it affects the other springs also. This results in what’s
called a ‘coupled’ system. That is, what happens to one truss member may affect another.
• With a little work (CES 4141) we can find three coupled equations that describe the behavior of this system
(how much does each spring stretch when we apply forces ?).
• Each equation uses the spring concept 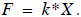The unknown displaced position of the ends of each
spring ( x ) after the forces are applied are then found by solving a system of linear equations.

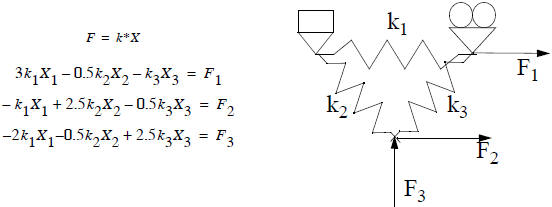
• These equations can be solved for 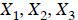by using matrix methods of solving simultaneous equations.
• once we solve for the displacements 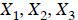, we can determine the internal forces in the truss and
design it to withstand the forces.

Curve Fitting

finding mathematical functions f(x) to describe observed behaviors
i.e. define a curve that fits some measured data

We will use the function f(x) to PREDICT future behavior.

ANALYTICAL :

• Sometimes an exact solutions (equation) can be derived using known physical laws .
e.g. beam deflection using continuum mechanics

NUMERICAL MODELS :

• Exact solution not known or too complex .
• Instead we approximate behavior by observing the process (taking data)
• Fit model to observed data.
e.g. force vs. displacement for steel
e.g. rocket velocity vs. time

• Recall the practive exam question about rocket performance with time

Let’s say an equation for vertical velocity as a function of time is given as:

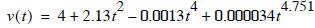
Where did this equation come from? Analytical or numerical model?
Suppose the rocket was launched and velocity was measured (poorly), giving the plot on the left :

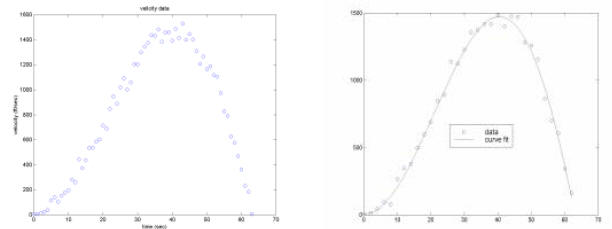
We then apply a numerical CURVE FITTING algorithm to the data. The outcome is the following equation

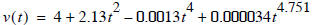shown with the data on the right

Root Finding

We now have the function (model) describing the rocket velocity as a function of time ( v(t) )
What can we do with it?

• Use the model to construct / define solutions

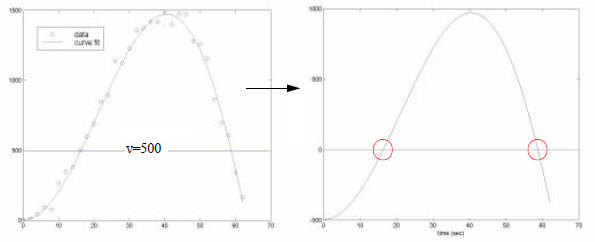
Suppose we need to know when velocity will reach 500 feet/sec. There are two ways to solve this problem

Problem: using 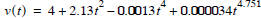, find the time at which velocity = 500 ft/sec.

Solution method #1: attempt to find an Analytical Solution
set the left hand side equal to 500 and solve for t 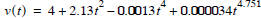,find t

Solution method #2: use Numerical Root Finding Method to find when v(t) = 500
Recast to find when function is equal to zero
find t such that v(t) - 500 = 0

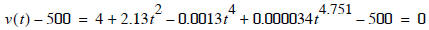
Now apply a ROOT FINDING method to identify where the curve crosses zero

Optimization - identifying minima / maxima

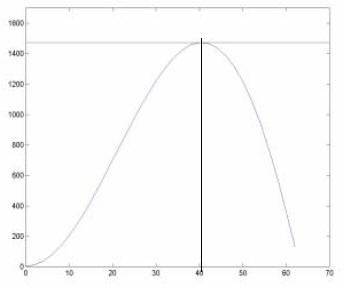
Suppose we need to know two more things about the model for rocket velocity:

Problem:
1) when the rocket will reach its maximum velocity?
2) what that maximum velocity will be?

Solution Method #1: Analytical Solution
We can find the maximum of a function using calculus
Take the deriveative of the function, set it to zero, and solve for t

Solution Method #2: Numerical Optimization Method to find the maximum of a curve
Optimization algorithm will locate the maximum value and the time it occurs

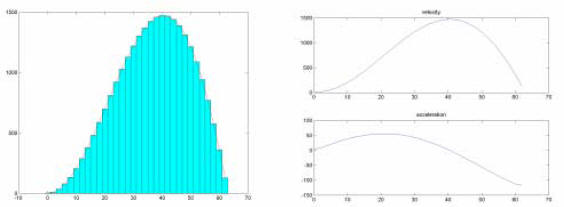
Integration / Differentiation

We have the velocity as a function of time v(t)
Suppose we want to estimate the rocket’s height and acceleration also...
• Integration of vertical velocity gives us height
• Differentiation of vertical velocity gives us vertical acceleration
Again, perhaps its possible to find an analytical derivative and integration.
But if that is impossible or overly complex, we can use numerical methods to approximate the results.

Ordinary Differential Equations:

Given the differential of a function at any point, and initial conditions
Find the function itself

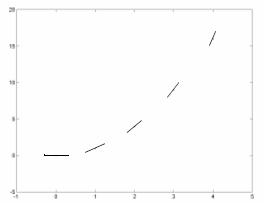
e.g. given 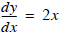and y(x=0) = 0

find the function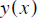
• All we have is the slope for any given x value
• We have to piece together the actual function
Analytical solution
or
numerical method

Real example :

building response to wind loads is described by a differential equation

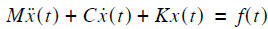
Given the building parameters K, C, M find the building displacement x due to wind forces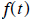

Probability / statistical analysis

The analyses of the behavior of systems should account in some manner for the uncertainties in the defining
parameters.

For example, let’s consider the cantilevered beam again. A
point load is placed at the tip, and deflection is measured there.

We calculate that if the deflection exceeds 10% of the length L
of the beam, then the system will break. That is,

failure = defl > 0.1*L

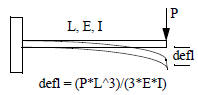
Deterministic case:

If we are given constant, known values for E, I, L, and P, we can calculate deflection and say ‘yes’ of ‘no’
to the question of failure.

Uncertain case:

However, its not always true that we know the exact values for these parameters. What if P is only an estimate,
how reliable is the estimate? Could it be off by 5% ? 20% ? What if E was an average value calcuated
from several batches of steel. Does this particular beam have a slightly higher or lower E value ?
How does this affect our ability to say ‘yes’ or ‘no’ to the failure question?

Probabilistic analysis:

The goal is to quantify the uncertainty in the given parameters.

Then we can then look at the deterministic question

Deterministic Q: Will the deflection exceed 10% of L ?

and re-phrase it to account for uncertainty:

Probabilistic Q: Given what we know about the uncertain quantities, what is the probability that deflection
exceeds 10% of L? This is no longer a ‘yes’ or ‘no’ question.

This represents the LIKLIHOOD of the beam failing given the uncertain information available.

This is also called Reliability analysis
We’ll spend some time discussing how to define and then answer such questions