Cartesian Coordinate System and Functions
Solutions to Exercises
8.1. Solutions: I’ll just use equation (1).
(a) P(0, 0) and Q(3,−4)
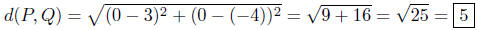
(b) P(−3, 4) and Q(−1,−1)
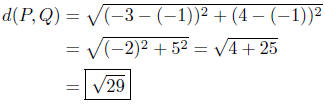
(c) P(−4, 2) and Q(5, 2)
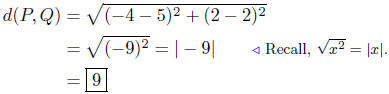
(d) P(−1, 5) and Q(7, 9)
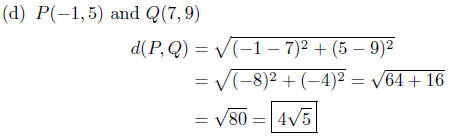
8.2. Solutions:
(a) Given P(0, 0), Q(1, 1) and R(2, 0), does PQR form a right triangle?
Solution: Verifythe following calculation:
d(P,Q) =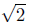
d(P,R) = 2
d(Q,R) =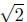
Note that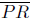 
is the longest side and
d(P,R)2 = d(P,Q)2 + d(Q,R)2
Thus, the points P, Q, and R form a right triangle.
(b) Given P(6,−7), Q(11,−3) and R(2,−2), does PQR form a right
triangle?
Solution: Verifythe following calculations:
d(P,Q) =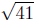
d(P,R) =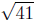
d(Q,R) =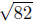
The side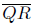 
is the longest side. Note that
d(Q,R)2 = d(P,Q)2 + d(P,R)2
Thus, the points P, Q, and R form a right triangle.
(c) P(1, 2), Q(−3, 4) and R(4,−2)
Solution: Verify the following calculations:
d(P,Q) =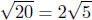
d(P,R) = 5
d(Q,R) =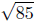
The side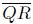 
is the longest side. Note that
d(Q,R)2 = 85 ≠ 45 = 20+25 = d(P,Q)2 + d(P,R)2
The square of the longest side does not equal to the sum of the
squares of the other two sides ; therefore, P, Q and R do not
form a right triangle.
8.3. Solutions:
(a) Given P(1, 3), Q(2, 5) and R(4, 9), is Q between P and R?
Solution:
d(P,Q) =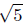
d(P,R) =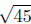
d(Q,R) =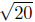
(Verifythese calculations.) Is it true that
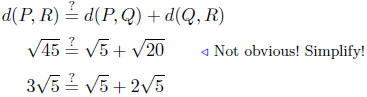
They are equal! Indeed, Q does lie between P and R.
(b) Given P(−1, 10), Q(2,−5), and R(5,−12), is Q between P and
R?
Solution:
d(P,Q) =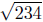
d(P,R) =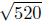
d(Q,R) =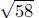
(Verifythese calculations.) Is it true that
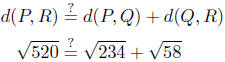
Make a calculator calculation to see that
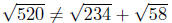
In this case, the left hand side is not equal to the right hand
side. Conclusion: Q is not between P and R.
8.4. Solution: The perimeter of a triangle is the sum of the lengths
of its sides.
Verifythe following calculations, and e-mail if I am in error.
d(P,Q) =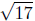
d(Q,R) =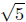
d(R, P) =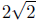 
The perimeter is
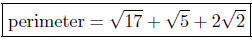
Question. Is this triangle a right-triangle?
(a) Yes
(b) No
8.5. Solution: I’ll take my own hint—I hope you did too.
Given: P(1 + t, 3 − t) and O(0, 0)
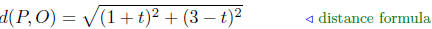
We want d(P,O) = 4, therefore,
Solve for t: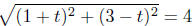
Square both sides of the equation, expand and combine .
 |
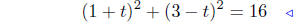square both sides |
 |
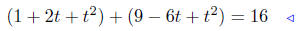expand |
 |
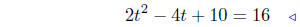combine |
 |
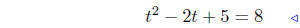divide both sides by 2 |
 |
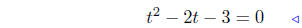subtract 18 from both sides |
We now solve the equation t2 − 2t − 3 = 0. We could use the
Quadratic
Formula; however, this is an equation that can be solved by
factoring:
t2 − 2t − 3 = 0
(t − 3)(t + 1) = 0
Therefore,
t = −1, 3
Presentation of Solution :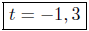 
There are actually two times at which the particle is exactly4 units
away from the origin.
8.6. Demonstration: Since the points are vertically oriented, x1 = x2:
 |
|
 |
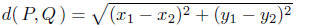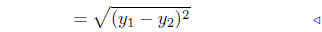since x1 = x2 |
 |
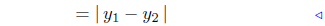by (1) of Lesson 2 |
8.7. Solution: We use equation (3) throughout these solutions.
(a) Given: P(1, 2) and Q(1, 9), compute d(P,Q). The first coordinates
are equal; therefore, these are verticallyorien ted points.
The distance between them is the upper most minus the lower
most:
d(P,Q) = |2 − 9| = 9−2 =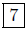 
(b) Given: P(−3, 3) and Q(−3,−4), compute d(P,Q). These points
are vertically oriented because the x-coordinates are equal.
d(P,Q) = |3 − (−4)| =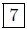 
(c) Given: P(4, 3) and Q(−3, 3), compute d(P,Q). Here, the second
coordinates are equal; these are horizontally oriented points.
d(P,Q) = |4 − (−3)| =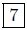 
(d) Given: P(π,−5) and Q(π,−2), compute d(P,Q). Vertically oriented
points.
d(P,Q) = | − 5 − (−2)| =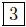 
What do you know about that, they’re all 7 units apart! Oops! All
but one—how did that one get in there!
8.8. Solutions: Hopefully you used formula
(4).
(a) Find the midpoint between P(−1, 3) and Q(5, 7).
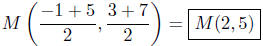
(b) Find the midpoint between P(2, 4) and Q(2,−5).
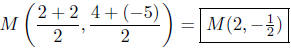
Did you note that these two points were vertically oriented? You
did, didn’t you.
(c) Find the midpoint between P(5,−3) and Q(12,−3).
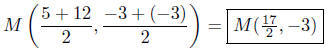
These were two horizontallyorien ted points.
(d) Find the midpoint between P(−1,−1) and Q(4, 2).
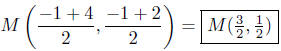
8.9. Solutions:
(a) Find the center and radius of the circle containing the points
P(1, 2) and Q(−3,−1), which are diametrically opposite.
Calculation of the Center: The radius is the midpoint of the line
segment PQ, since the points lie of the same diameter.
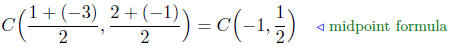
Radius Calculation: The radius is one-half the diameter. Thus,
from the distance formula , we have
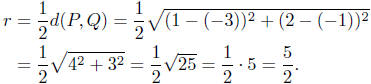
Presentation of Answer:
Center: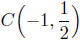 
Radius: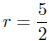
(b) Find the center and radius of the circle containing the points
P(−1, 4) and Q(0, 0), which are diametrically opposite.
Calculation of the Center: Again, the center is midway between
the endpoints of any of its diameters.
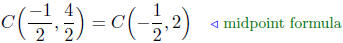
Calculation of the radius: The radius is one-half the diameter.
By the distance formula, we have
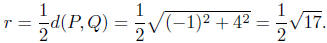
Presentation of Answers:
Center: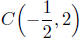 
Radius: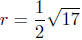 
8.10. Solutions: Just use the replacement technique. Be sure to verify
these calculations.
(a) Given f(x) = 2x2 − 3x; evaluate f(2), f(−2), f(−1/2).
f(2) = 2 · 22 − 3 · 2 = 2
f(−2) = 2(−2)2 − 3(−2) = 14
f(−1/2) = 2(−1/2)2 − 3(−1/2) = 2
(b) Given g(s) = s(s + 1)(s + 2); evaluate g(0), g(1), g(−1), g(−3).
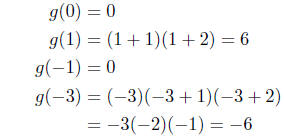
(c) Given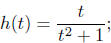 
evaluate h(1), h(−2), h(1/2), h(−1/2).
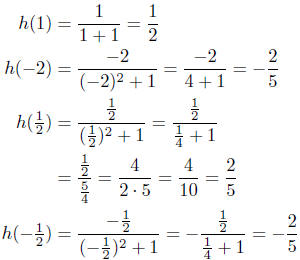
(d) Given D(w) =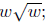
evaluate D(9); D( 1/9 ).
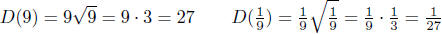
8.11. Solution to: (a) Find the domain of f(x) = |x − 1|. Here, the
natural domain is all of R, the real number line.
Dom(f) = R.
This is because there are no constraints on the value of x . For any x
we can calculate x − 1 and then calculate its absolute value |x − 1|.
Solution to (b) Find the domain of
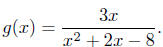In this problem,
we just must make sure the denominator is never equal to zero .
To identifythese x’s, we find where x2 + 2x − 8 = 0.
Solve:
 |
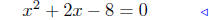given |
 |
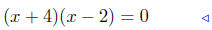factor |
 |
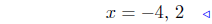the solutions |
Presentation of Solution:
 |
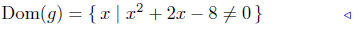initial description |
 |
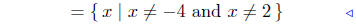set notation |
 |
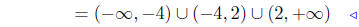interval notation |
Solution to (c) Find the domain of
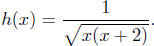Based on the
strategy, we see there are a number of constraints on the values of x:
x ≠ 0
x ≠ −2
x(x + 2) ≥ 0
These three can be summarized by a single inequality :
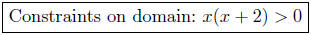
We use the Sign Chart Method to analyze x(x + 2).
The Sign Chart of x(x + 2)
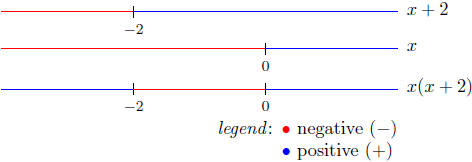
Presentation of Solution:
 |
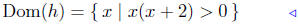initial description |
 |
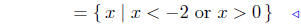set notation |
 |
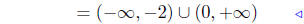interval notation |
Solution to (d) Find the domain of
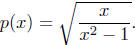From the basic
strategy, we see that
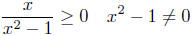
Realizing that x2 −1 ≠ 0 is equivalent to x ≠ −1 and x ≠ 1 is see . . .
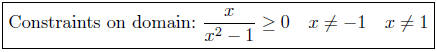
Begin by doing a Sign Chart Analysis on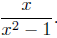 
The first step is to factor completely.
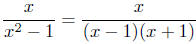
It is to this expression that we now apply the method.
The Sign Chart of
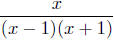
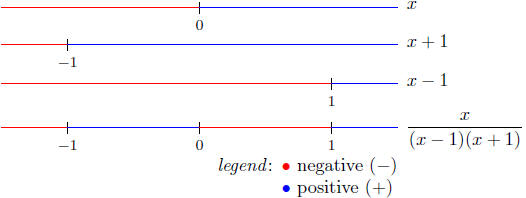
Taking the blue line as our solution, and keeping in mind that x ≠ −1
and x ≠ 1 we get
 |
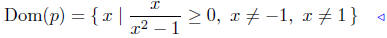initial description |
 |
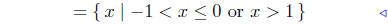set notation |
 |
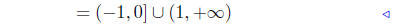interval notation |
8.12. Solutions:
(a) f(x) = 4x − 1
 |
|
 |
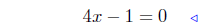substitute |
 |
add 1 to both sides |
 |
divide by 4 |
Presentation of Answer: The x-intercept is
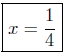
(b) f(x) = x2 − 3x + 2
 |
|
 |
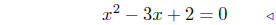substitute |
 |
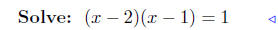factor |
 |
solved! |
Presentation of Answer: The x-intercepts are
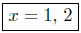
(c) f(x) = x3 + 6x2 ++8x
 |
|
 |
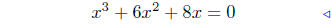substitute |
 |
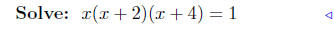factor |
 |
solved! |
Presentation of Answer: The x- intercepts are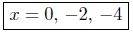 
(d) f(x) = x2 + x + 1
 |
|
 |
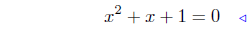substitute ( quadratic equation ) |
 |
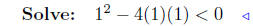negative discriminant |
No Solutions
Presentation of Answer: The function does not cross the x-axis.
Solutions to Exercises
(e) f(x) = 2x2 − x − 1
 |
|
 |
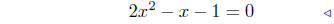substitute |
 |
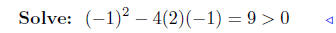positive discriminant |
 |
quadratic formula |
 |
simplify |
 |
Note: This equation could have also been solved byfactoring
the left-hand side.
Presentation of Answer: The x-intercepts are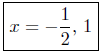 
(f) f(x) = x2 + x − 3
 |
|
 |
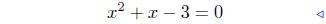substitute |
 |
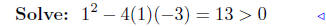positive discriminant |
 |
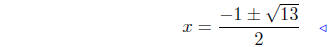quadratic formula |
Presentation of Answer: The x-intercepts are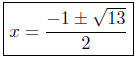 
| Prev | Next |