Cengage Now Hints for Lesson 11, 12 and 13

In general:

You can use the discussion board to post questions and/or read responses. Josh will be live
on that board MWF from 6-8 pm all semester. If you post a question at a different time ,
he will respond as soon as he is able. Do not post after 8:00 pm on a due night and
expect an immediate answer. He will not help you as a tutor, but may provide some
hints. Please do not expect him to solve things for you.

In general, use Mozilla browser with a PC. Internet Explorer can cause technical issues
with Cengage Now problems. We recommend using an ITAP computer or following the
configuration instructions on the Cengage Now homepage.

If you log in and see a message that says popups are blocked, enter Cengage Now
anyway. That error does not affect your assignments. However, a current version of Java
must be installed for Cengage Now to work properly. If the system check detects a Java
problem, follow the instructions given to correct that.

You can always view the correct answer to each problem after submitting the assignment.
Click on “view assignment details”. It will show you what you entered and what the
correct answer was. If you log back into the assignment, you will get a different version
of the problems that were not correct. Correct problems stay correct and you do not redo
them.

Lesson 11:

For equations using the quadratic formula, you must simply your answer as much as
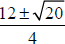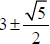possible before entering. For example, must be simplified to or


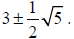
#4: To enter a subscript, 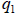, for example, type q then choose 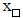from under the log x
menu. Math hint : Remember that all values represent positive quantities so we disregard
the negative square root and only use the positive. Do NOT rationalize the denominator
and you can leave the fraction under one square root .

#5: It is easier to leave the ½ instead of multiplying both sides by 2. Subtract the s to the
right side and use the quadratic formula. This is a fairly difficult problem. To enter a
subscript and an exponent, use 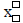option under the log x menu. Again, all values
represent positive quantities so disregard the negative square root .

#7: Math hint: When solving the equation, one of the answers does not make practical
sense to the application problem. Choose the solution that does make sense and find the
dimensions of the sheet of paper. For example, since the length was twice the width, if
my answer that made sense was 9, the dimensions are 9 by 18.

Lesson 12:

#1: Math hint: You will use the quadratic formula to solve for t. Round answers to three
decimal places .

#2 (b) Math hint: This equation will factor by trial and error to find v. Remember to
disregard the answer that does not make practical sense to the problem.

#4 and 5: This problem could factor by trial and error, but it is probably easier to use the
quadratic formula. Remember to disregard the answer that does not make
practical sense to the problem.

#7: Math hint: Remember that the rate given is mph (miles per hour) and therefore, your
answer will be in terms of hours. To round to the nearest minute, you must multiply
your answer by 60, then round to the nearest minute.

#8: If no pizza box picture shows, refer to #71 in the textbook on page 86 for the picture
of the pizza box. All the numbers you will need are shown online.

Lesson 13:

#1,2 and 3: Enter the answer in the form a+bi (no factoring of common factors). Use
lower case i as the imaginary unit.

#6 and 7: Math hint: Remember to use the conjugate of the denominator. Then be sure
to write your answer in the form a+bi. For example, to write 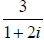in the
form a+bi, I multiply the numerator and denominator by 1− 2i . The result is
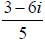. To enter online, it must be written as a+bi, or 3/5-6/5i. The same
would be true on an exam.

#8: Math hint: Before you FOIL, be sure to change the radicals to their imaginary
counterparts. For example, 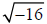is 4i.

#9: Math hint: If two imaginary numbers are equal to each other, then their real parts
have to be equal as do the imaginary parts. For example, if (2x − y) −16i =10 + 4yi ,
then 2x − y =10 and −16i = 4yi . Then you can solve for x and for y (solve for y
first).