Get it on Google Play Get it on Apple Store

Sample Problems for Math 111 Test 1 Solutions

1. Find the slope of a line through the points (2,−3) and (5, 1).
Solution: Slope is given by the difference of the y - coordinates divided
by the difference of the x-coordinates, so the slope is given by

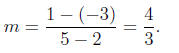
2. List all possibilities for the number of solutions that a system of 3
equations in 3 unknowns can have. Does this answer change (and if so
how) if we have 3 equations in 4 unknowns?
Solution: If the number of equations is greater than or equal to the
number of unknowns (as is the case for 3 equations and 3 unknowns)
the possibilities are:
• 0 solutions,
• Exactly 1 solution, or
• Infinitely many solutions.

In the latter case, there are more unknowns than equations, so there
are only two possibilities :
• 0 solutions, or
• infinitely many solutions

3. Write the augmented matrix associated to the equations

2x + 4y − z = 1
3x − 2y + z = 2
5x − y = −2

Solution:

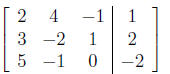
4. If a graph has a negative slope , as you move to the right on the graph,
do the y- values get larger or smaller?
Solution: As the x-values get larger, the y-values get smaller. Since
the x-values get larger as you move to the right, the y-values get smaller.

5. If

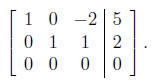
is the reduced row echelon form of the matrix A associated to a system
of equations (in x, y, and z), write the solution of the corresponding
system of equations .
Solution:

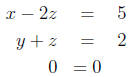
Do remember to include the third equation.

6. What are the three different forms for the equation of a line.
Solution: We actually gave 4 in class, and I would accept any 3 of the
4. They are
• Slope-intercept: y = mx + b.
• Point-slope: y − y1 = m(x − x1).
• General form: Ax + By + C = 0 (or alternatively Ax + By = C I
would accept one or the other, but they count as the same form).
• Intercept Form: 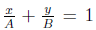(where A and B are the x- and y-intercepts).

I would also accept the two-point version of a line, but I would prefer
the one’s above.

7. Write down a matrix in row-reduced form for which the corresponding
system of equations has NO solutions.
Solution: The easiest system would have only one equation, but to
be slightly interesting:

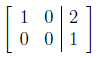
8. Write down a matrix in row-reduced form for which the corresponding
system of equations has infinitely many solutions.
Solution: We need a column without a leading 1. So for example:

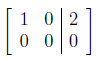
Solution: Using that A−1A = I3 the 3 × 3 identity matrix, then

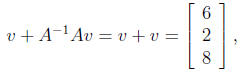
9. Are the two matrices below inverses? Explain how you know.

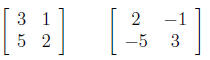
Solution: Yes they are inverses. We know that is true by multiplying
the two matrices and seeing that we get the identity matrix out. To
see that:

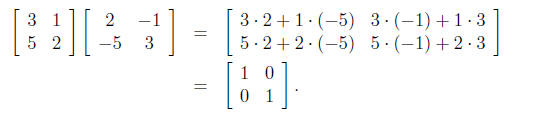
10. Determine graphically the solution set for each system of inequalities
and indicate whether the solution set is bounded or unbounded:

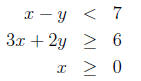
Solution: The solution is unbounded. To solve it graphically, you
need to graph the three lines: x−y = 7 (which passes through (0,−7)
and (7, 0), graphed with a dashed line), the line 3x + 2y = 6 (which
passes through (0, 3) and (2, 0), and the line x = 0 (the y-axis). After
checking a test point, we see that the solution is the shaded region to the
upper right of the triangle. including the two solid lines as boundary.
(I will try and get a picture solution on the web soon, but I am having
trouble getting one converted to the type of file I need to do so.)

11. True or False ( Circle the letter ). Partial credit will be given only if an
explanation is included.

T F The matrix 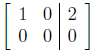corresponds to a system of equations
with no solutions.
Solution: False, the equations become x = 2 and 0 = 0. Since
we don’t have a contradiction in the equations, and there are
two variables with the second column has no leading 1, there are
infinitely many solutions

T F The matrix 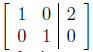 corresponds to a system of equations
with exactly one solution.
Solution: True. The corresponding equations are: x = 2 and
y = 0 and there are exactly 2 variables there is a unique solution.
Alternatively, since every column to the left of the vertical line has
a leading 1 and there is not a row with corresponding equation
0 = 1, there must be a unique solution.

T F The matrix is in row-reduced echelon form.
Solution: False. The first non- zero entry in the last row is a 2,
not a 1 as required.

T F The matrix 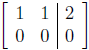is in row-reduced echelon form.
Solution: True. Every row has a leading 1 and the column with
the leading 1 has 0s elsewhere.

T F If A is an m×n matrix and B is an m×k matrix, then AB
is an n × k matrix.
Solution: False, you cannot multiply A and B since A has a
different number of columns as B has rows (unless m = n).

12. If 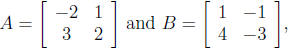find the product matrix AB.
Solution: The product of the matrices is given by

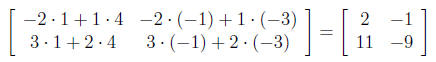
Calculator and Study Sheet Allowed

13. Write the equation of the line passing through the points (3, 5), and
(−3, 17).
Solution: The slope of the line is given by

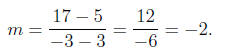
Using the point-slope equation of the line we obtain
(y − 5) = −2(x − 3).

14. What is the slope of the line 3x + 5y = 9?
Solution: We could rewrite the line in point slope form, find two points
on the line and calculate the slope from those points, or remember the
formula for finding the slope from the general equation of a line. In
any case, the answer is that the slope is

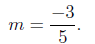
15. A manufacturer has monthly fixed costs of 2, 600 and a production cost
of $2 for each unit produced. If the product sells for 5 per unit, write
(a) The cost function C(x).
(b) The Revenue Function R(x).
(c) The Profit Function P(x).
(d) What is the break-even point for this system?
(e) The Profit at the break-even point is.
Solutions: The fixed cost F = 2600 and unit cost 2. Thus the cost
function is given by
C(x) = 2x + 2600.
Since each unit sells for 5 dollars, the revenue function is
R(x) = 5x.
The Profit function is the difference of the revenue and the cost, so
P(x) = R(x) − C(x) = 3x − 2600.

The break-even point is where the cost equals the revenue. Thus we
solve the equation:
5x = 2x + 2600.
Solving we get

3x = 2600 subtracting 2x from both sides

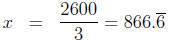dividing by 3.

Since we are selling units and presumably cannot sell 2/3 of a unit, I
would accept either 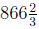or 867 units. The profit at this point is then
given by

P(867) = 3(867) − 2600 = 1.

That is the profit at the ”break-even” point is 1 dollar if we take 867.
More typically we would have that the break even point would have a
profit of 0 dollars, which is what happens at

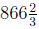
Prev Next