Solving Equations
Solving Equations : The Addition Property
Definitions
 An equation is a
mathematical statement in which two
An equation is a
mathematical statement in which two
expression shave the same value .
Example: 3x + 4 = 2x + 10
 The solution of an equation is a value
of the variable that
The solution of an equation is a value
of the variable that
makes the equation a true statement .
Is 6 is a solution of 3x + 4 = 2x + 10?
Determining Solutions
To determine whether is 6 is a solution of 3x+4=2x+10,
we substitute 6 for x in the equation and simplify.
 Ifbothsidesareequal,6isasolution.
Ifbothsidesareequal,6isasolution.
 Ifbothsidesarenotequal,6isnotasolution.
Ifbothsidesarenotequal,6isnotasolution.
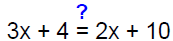 |
|
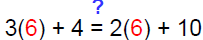 |
 Substitute 6
for each x Substitute 6
for each x |
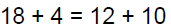 |
 Simplify Simplify |
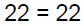 |
 True! True! |
Solving Equations
 Goal: Get the variable
alone on one side of the equation and a
Goal: Get the variable
alone on one side of the equation and a
number on the other side so the equation reads:
variable = number
 Tools: Addition and
Multiplication Properties
Tools: Addition and
Multiplication Properties
We use the Addition Property to move terms
from one side
of the equation to the other side.
We use the Multiplication Property to solve
for the variable or
rewrite an equation.
The Addition Property of Equality
For all real numbers a, b, and c ,
if a = b, then a + c = b + c
The same number may be added or subtracted on both sides
of an
equation with out changing the solution .
![]() To solve an equation
using the addition property, add (or
To solve an equation
using the addition property, add (or
subtract) to get the variable term alone on one side of the
equation and the number on the opposite side.
Numbers on both sides?
Move the number.
Example 1 Solve:−15 + x = 37
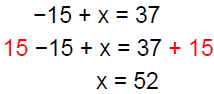 |
alone on one side. |
Variable terms on both sides?
Move the variable term.
Example 2 Solve: 2k = −16 + k
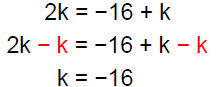 |
alone on one side. |
Numbers and variables on both sides?
1) Move the variable term to one side.
2) Move the number to the opposite side.
Example 3 Solve: 4y + 1.8 = −5.4 + 3y
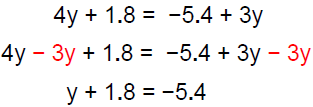 |
y alone on one side. |
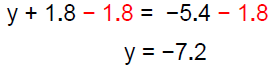 |
the number to the other side. |
Hint: Moving the smaller variable term over to the larger,
keeps
the variable term positive !
Practice Exercise 1
Solve: −7= b + 15
A.22
B.8
C.−8
D.−22
Practice Exercise 2
Solve: 4y= 3y − 5.7
A.−5.7
B.57
C.5.7
D.−57
Practice Exercise 3
Solve: 3z + 2.5 = 1.4 + 2z
A.−3.9
B.−1.1
C.3.9
D.1.1
Simplifying Equations
Combine like terms on the same side. (Don't add opposites!!) Then
use the addition property to move terms.
Example 4 Solve: 6 – 3x = 7x – 8 – 9x
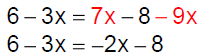 |
|
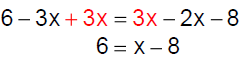 |
variable term. |
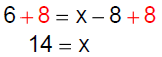 |
number. |
Removing Parentheses
Use the distributive property to remove parentheses.
Example 5Solve: 6(x −2) + 5 = 5(x + 3)
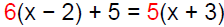 |
|
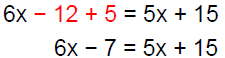 |
|
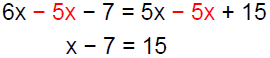 |
|
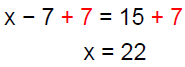 |
|
Practice Exercise 4
Solve: 7x –6 + 2x = 2 + 8x –12
A.4
B.8
C.−8
D.−4
Practice Exercise 5
Solve: 8(x −2) = 7(x −3)
A.5
B.−37
C.−5
D.1
Practice Exercise 6
Solve: −3(m + 5) = 7 − 4(3 + m)
A.10
B.−10
C.20
D.5
Solving Equations with Fractions
Example 6 Solve: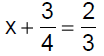
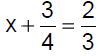 |
|
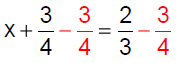 |
|
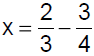 |
|
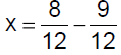 |
|
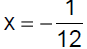 |
Practice Exercise 7
Solve: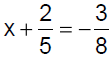
A. −5/13
B. 1/40
C. −31/40
D. −1/3
Practice Exercise 8
Solve: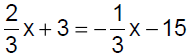
A. −12
B. −18
C. 18
D. 12
Solution − Practice Exercise 1
Solve: −7= b + 15
Answer: D
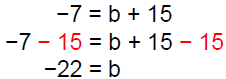 |
|
Solution − Practice Exercise 2
Solve: 4y= 3y − 5.7
Answer: A
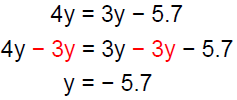 |
|
Solution − Practice Exercise 3
Solve: 3z + 2.5 = 1.4 + 2z
Answer: B
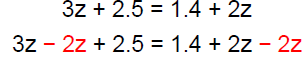 |
|
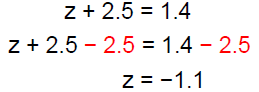 |
|
Solution − Practice Exercise 4
Solve: 7x −6 + 2x = 2 + 8x −12
Answer: D
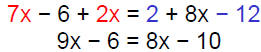 |
|
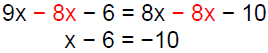 |
|
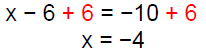 |
Add 6 on both sides. |
Solution − Practice Exercise 5
Solve: 8(x −2) = 7(x −3)
Answer: C
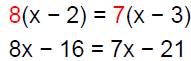 |
|
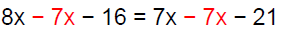 |
|
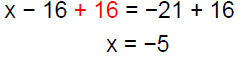 |
|
Solution − Practice Exercise 6
Solve: −3(m + 5) = 7 − 4(3 + m)
Answer: A
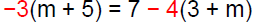 |
|
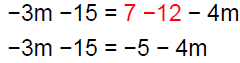 |
|
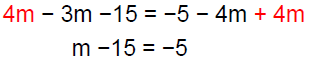 |
|
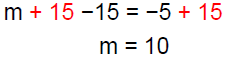 |
|
Solution − Practice Exercise 7
Solve: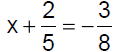
Answer: C
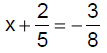 |
|
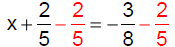 |
|
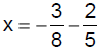 |
|
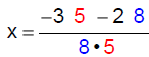 |
multiply to get the numerators |
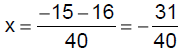 |
|
Solution − Practice Exercise 8
Solve: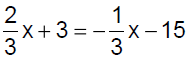
Answer: B
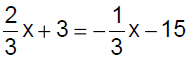 |
|
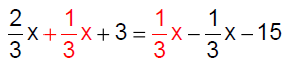 |
Add 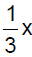 on both
sides. on both
sides. |
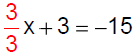 |
Simplify. |
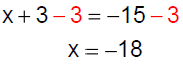 |
Subtract 3on both sides. |
| Prev | Next |