Direct Proof

The simplest and most straightforward type of proof is a \direct" proof, which we'll call
any proof that follows straight from the definitions or from a direct calculation . Here's a
couple of examples:

First we'll prove the following statement:

The sum of any two rational numbers is rational.

This proof follows directly from the definition of what it means for a number to be rational .

Given that: r and s are rational numbers.

Show that: r + s is rational.

Proof: Since r and s are rational, we can write r = p/q and s = m/n for
some integers p, q, m, and n.

Then .

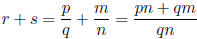Since p, q, m, and n are integers, pn+qm and qn are also integers ( the sum
or product of integers is an integer). Thus by the calculation above, r +s is
the quotient of two integers , and is therefore a rational number .

Here's an example of a proof that is really just a calculation. Given the trigonometric
identity sin(x + y) = sin x cos y + cos x sin y, we'll prove the identity:

sin(2x) = 2 sin x cos x

Given that: sin(x + y) = sin x cos y + cos x sin y.

Show that: sin(2x) = 2 sin x cos x.

Proof:

sin(2x) = sin(x + x)
= sin x cos x + cos x sin x (by the sum identity )
= 2 sin x cos x:

Note that this proof is merely a string of equalities connecting sin(2x) to 2 sin x cos x. Many
proofs are like this ; when proving an identity or an equation we often start from one side
of the equation and work towards the other.