Summary of Results for First 3 Lectures

We have followed Section 3.1 and 4.4 of the text [1].

I. DISCRETE TIME QUEUES AND STABILITY (SECTION 3.1 OF TEXT)

A. Discrete Time Queues

One- Step Dynamic Equation for Discrete Time Queues:



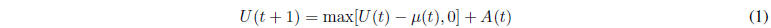
Sample path inequality :


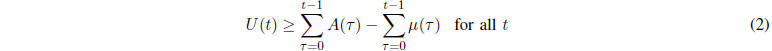
B. Strong Stability

Definition 1: A discrete time queue with backlog process U(t) is strongly stable if:



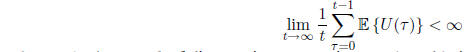
Definition 2: A network of discrete time queues is strongly stable if all individual queues are strongly stable.
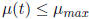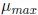Lemma 1: Suppose that  for all t (for some finite bound ). Then if U(t) is strongly stable, we
have:
 

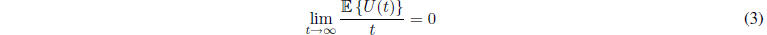
Proof: The proof is beyond the scope of this course. The interested reader can find the proof in the appendix
of [2].

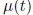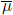We had definitions of and A(t) being admissible with rates and 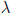, respectively (given in Section 3.1 of
text). The 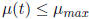assumption is part of admissibility, and will be assumed to hold throughout this course.
Note that if 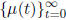is an i.i.d. sequence with a bounded 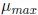, then it is admissible. Likewise, if 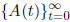is
an i.i.d. sequence with bounded first and second moments, then it is admissible.

Theorem 1: (Stability Theorem) If A(t) is admissible with rate 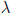and 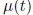is admissible with rate 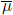, then:
(a) Strong Stability implies that 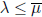(and 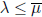so is necessary for strong stability).
(b) 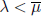implies strong stability (and so 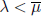is sufficient for strong stability).

Note there is a "singularity" between necessity and sufficiency for 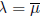. In this case, there are examples where
the queue is strongly stable, and there are other examples where the queue is not strongly stable.

Proof: The proof of part (a) uses (2) together with the fact that (3) holds for strongly stable queues. You are
expected to know the proof.

The proof of (b) was done in class for the i.i.d. case, using Lyapunov drift theory. You are also expected to know
the proof for this i.i.d. case. The proof for the non-i.i.d. case is given in Section 4.4 of the text using the idea of
T-slot Lyapunov drift.

Note that throughout this course we shall use the term "stability" to refer to strong stability.

II. LYAPUNOV DRIFT (SECTION 4.4 OF TEXT)

Let 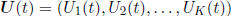represent a vector process of queue backlogs that evolve in discrete time
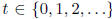. Let L(U) represent a non- negative function , called a Lyapunov function, of the queue backlog
vector. Define the one-step conditional Lyapunov drift as follows:

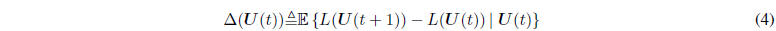
Theorem 2: (Lyapunov Drift) Suppose that U(t) evolves according to some probability law , and suppose there
exists a non-negative function L(U) and constants B < ∞ and ε > 0 such that for all timeslots t and all possible
values of U (t), we have:

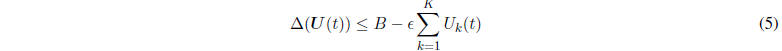
Then the queueing network is strongly stable (i.e., all queues are strongly stable), and:



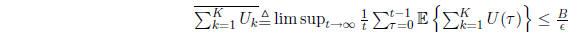
Proof: You are expected to know the proof. The proof uses 2 main concepts:

1) Iterated Expectations: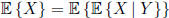

2) Telescoping Sums :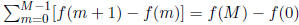

A typical Lyapunov function that is very useful is the following quadratic function :

A fact that is often useful in dealing with quadratic Lyapunov functions: If 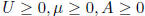then:



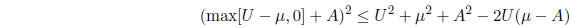
This fact is used together with the Lyapunov Drift Theorem to prove part (b) of Theorem 1.

III. SOME COMMENTS ABOUT LYAPUNOV FUNCTIONS, DELAY, AND COMPLEXITY

Lyapunov drift for network stability is first used in [3] for multi-hop networks, and in [4] for opportunistic
downlink scheduling. Related quadratic Lyapunov functions are used to make stability and delay claims for N × N
packet switches in [5] and for multi-hop mobile networks in [6]. Non-quadratic Lyapunov functions can sometimes
be used to make modified or improved statements about delay [7] [8] [9]. Alternative Lyapunov functions via queue
groupings can often lead to improved complexity and/or delay bounds, see [10] [11] [12] [13].

Performance optimal Lyapunov networking will be a large part of this course and will likely be useful for your
projects. However, we will not get to this for another few weeks. Students can always read ahead in the text, and
are also referred to [2] for a writeup that emphasizes average power minimization and virtual power queues, which
is not covered in as much detail in the text.

REFERENCES

[1] L. Georgiadis, M. J. Neely, and L. Tassiulas. Resource allocation and cross-layer control in wireless networks. Foundations and Trends
in Networking, vol. 1, no. 1, pp. 1-149, 2006.
[2] M. J. Neely. Energy optimal control for time varying wireless networks. IEEE Transactions on Information Theory, vol. 52, no. 7, pp.
2915-2934, July 2006.
[3] L. Tassiulas and A. Ephremides. Stability properties of constrained queueing systems and scheduling policies for maximum throughput
in multihop radio networks. IEEE Transacations on Automatic Control, vol. 37, no. 12, pp. 1936-1949, Dec. 1992.
[4] L. Tassiulas and A. Ephremides. Dynamic server allocation to parallel queues with randomly varying connectivity. IEEE Transactions
on Information Theory, vol. 39, pp. 466-478, March 1993.
[5] E. Leonardi, M. Mellia, F. Neri, and M. Ajmone Marsan. Bounds on average delays and queue size averages and variances in
input-queued cell-based switches. Proc. IEEE INFOCOM, 2001.
[6] M. J. Neely, E. Modiano, and C. E Rohrs. Dynamic power allocation and routing for time varying wireless networks. IEEE Journal
on Selected Areas in Communications, vol. 23, no. 1, pp. 89-103, January 2005.
[7] N. Kahale and P. E. Wright. Dynamic global packet routing in wireless networks. Proc. IEEE INFOCOM, 1997.
[8] S. Shakkottai, R. Srikant, and A. Stolyar. Pathwise optimality of the exponential scheduling rule for wireless channels. Advances in
Applied Probability, vol. 36, no. 4, pp. 1021-1045, Dec. 2004.
[9] M. J. Neely. Super-fast delay tradeoffs for utility optimal fair scheduling in wireless networks. IEEE Journal on Selected Areas in
Communications, Special Issue on Nonlinear Optimization of Communication Systems , vol. 24, no. 8, pp. 1489-1501, Aug. 2006.
[10] X. Wu, R. Srikant, and J. R. Perkins. Scheduling efficiency of distributed greedy scheduling algorithms in wireless networks. IEEE
Transactions on Mobile Computing, June 2007.
[11] S. Deb, D. Shah, and S. Shakkottai. Fast matching algorithms for repetitive optimization: An application to switch scheduling. Proc.
of 40th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, March 2006.
[12] M. J. Neely. Delay analysis for maximal scheduling in wireless networks with bursty traffic. Proc. IEEE INFOCOM, April 2008.
[13] M. J. Neely. Order optimal delay for opportunistic scheduling in multi-user wireless uplinks and downlinks. Proc. of Allerton Conf.
on Communication, Control, and Computing (invited paper), Sept. 2006.