Dividing Polynomials
In this section, you’ll learn two methods for dividing
polynomials , long division and
synthetic division . You’ll also learn two theorems that will allow you to
interpret results
when you divide.
Suppose P(x) and D(x) are polynomial functions and D(x) ≠ 0. Then there
are unique
polynomials Q (x) (called the quotient) and R(x) (called the remainder) such that
P(x) = D(x) *Q(x) + R(x) . We call D(x) the divisor.
The remainder function, R(x) , is either 0 or of degree less than the degree of
the divisor.
You can find the quotient and remainder using long division. Recall the steps
you
learned in elementary school to perform long division:
Example 1: Find
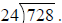
You can use the same steps when using long division to
divide polynomials.
Example 2: Find the quotient and the remainder using long division:
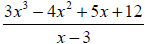
Example 3: Use long division to find the quotient
and the remainder:
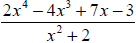
Example 4: If D(x) = 2x - 5 , Q(x) = 3x2 + 5x and
R(x) =12 , find P(x).
Often it will be more convenient to use synthetic division to divide
polynomials. This
method is easy to use, as long as your divisor is x ± c , for any real number c.
Synthetic division is best demonstrated by example, so here are a few:
Example 5: Find the quotient and the remainder using synthetic division:
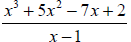
Example 6: Find the quotient and the remainder using
synthetic division:
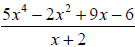
Example 7: Find the quotient and the remainder using
synthetic division:
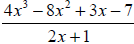
Example 8: Find the quotient and the remainder using
synthetic division: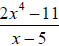
Here are two theorems that can be helpful when working
with polynomials:
The Remainder Theorem: If P(x) is divided by x - c , then the remainder is P(c)
.
The Factor Theorem : c is a zero of P(x) if and only if x - c is a factor of P(x)
, that is
if the remainder when dividing by x - c is zero .
You can use synthetic division and the remainder theorem to evaluate a function
at a
given value .
Example 9: Use synthetic division and the remainder theorem to find P(3) for
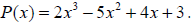
Example 10: Use synthetic division and the remainder
theorem to find P(-1) for
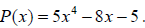
Example 11: Determine if x + 2 is a factor of
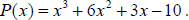
Example 12: Show that x = -1is a zero of
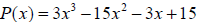and find the
remaining zeros of the function .
Example 13: Show that x = 2 and x = -3are zeros of
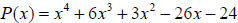and find the remaining zeros of the function .
Finally, you’ll need to work backwards to write a
polynomial with given zeros.
Example 14: Find a polynomial of degree 4 with zeros at -3, -1, 2 and 5.
Example 15: Find a polynomial of degree 3 with zeros at 0, 2 and -3.
| Prev | Next |