Exploring Ideas of Algebra and Coordinate Geometry
13.4 Connecting Algebra and Geometry
13.4.1. Finding the midpoint of a line segment
13.4.1.1. Theorem for coordinates of the midpoint : If the coordinates for the
endpoints of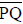 
are
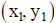for P and 
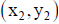for Q, then the
coordinates of the midpoint , M, of 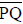are
13.4.2. Finding the distance between two points
13.4.2.1. Pythagorean Theorem = a2 + b2 = c2
13.4.2.1.1. for right triangles only
13.4.2.1.2. a and b are legs of the triangle – the sides that form the right
angle
13.4.2.1.3. c is the hypotenuse – the side opposite the right angle and
the longest side of the triangle
13.4.2.2. Distance Formula based on the Pythagorean Theorem
13.4.2.3. Distance Formula: If d is the distance between points
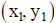and
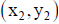, then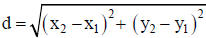 
13.4.3. Finding the equation of a line
13.4.3.1. Slope- intercept method
13.4.3.1.1. Slope is designated as “m”
13.4.3.1.1.1.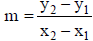 
13.4.3.1.2. Slope- Intercept form of a line
13.4.3.1.2.1. (0,b) is the y-intercept
13.4.3.1.2.2. y = mx + b
13.4.3.2. Two point method
13.4.3.3. Given and
, then
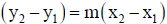
13.4.3.3.1. First, solve for m to obtain the slope of the line
13.4.3.3.2. Next choose
(arbitrarily could choose
if
desired, but can ONLY choose one point)
13.4.3.3.3. Then 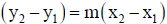and solve for y to put the equation
into slope-intercept form
13.4.3.3.4. Leave fractions in improper form – do NOT convert to mixed
numbers
13.4.3.4. Point slope method
13.4.3.4.1. Given m and
, the equation for a line can be found
by: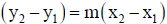
13.4.3.4.2. Solve for y to put the equation into slope-intercept form
13.4.3.5. Finding the point of intersection of two lines
13.4.3.5.1. First find the equation of each line:
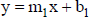and
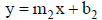
13.4.3.5.2. Next, use substitution to solve for x:
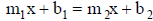
13.4.3.5.3. After finding x, choose either original equation to solve for y,
say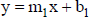
13.4.3.5.4. The x and y you found are the (x ,y) of the point of
intersection between the two lines
13.4.3.5.5. What happens when the slopes are equal?
13.4.3.6. Horizontal and vertical lines
13.4.3.6.1. Horizontal line properties
13.4.3.6.1.1. The slope of every horizontal line is in the form: y = b,
where (0,b) is the y-intercept
13.4.3.6.1.2. The slope of every horizontal line is zero
13.4.3.6.2. Vertical line properties
13.4.3.6.2.1. The slope of every vertical line is in the form: x = t,
where (t,0) is the x-intercept
13.4.3.6.2.2. The slope of every vertical line is undefined; a vertical
line has no slope
13.4.4. Using coordinate geometry to verify geometric conjectures
13.4.4.1. skip
13.4.5. Developing the equation of a circle
13.4.5.1. Circle equation theorem 1: The standard form for an equation of a
circle with a center at the origin and radius r is: x2 + y2
= r2
13.4.5.2. Circle equation theorem 2: The standard form for an equation of a
circle with a center at (h, k) and radius r is:
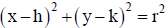
13.4.6. Describing transformations using coordinate geometry
13.4.6.1. skip for now – will include with transformations later
| Prev | Next |