Fractions

Section 1: Introduction

Recall that the set of whole numbers, W = {0, 1, 2, 3, 4,...}, was extended to the set of integers Ι = {...,-2, -1, 0, 1, 2,
...} . In this unit we extend the set of integers to a number system called the rational numbers. Rational numbers
were developed because there are instances when whole numbers and integers cannot fully describe or quantify
the situation. For example, how would you describe the portion of the large rectangle shaded in the following
diagram?

xxxxxxxxxxxxx	xxxxxxxxxxxxx
xxxxxxxxxxxxx

You can see that we have to extend the integers in order to handle a situation like this.

Definition: A fraction is a number of the form a/b, where a and b are integers and b ≠ 0.

Some examples of fractions are :

Definition: For the fraction a/b, a and b are called the terms of the fraction.
More specifically, a is called the numerator and b is called the denominator.

Example 1:

The terms of the fraction 2/3 are 2 and 3. The 2 is called the numerator, and the 3 is
called the denominator .

Example 2:

An integer such as 5 may also be put in fraction form, since 5 can be written as 5/1. In this
case, 5 is the numerator, and 1 is the denominator.

Definition: A proper fraction is a fraction in which the numerator is less than the denominator. If the
numerator is greater than or equal to the denominator, the fraction is called an improper fraction.

In example 1, 2/3 is a proper fraction and in example 2, 5/1 is an improper fraction.

Section 2: Fraction Models

There are three categories of models used in developing fraction concepts: area models, set models, and length or
measurement models. We will try to use all three models in our development of fractions.

When using the three models for fractions,

1) we have to identify what the "whole" or "1" is,
2) we divide the "whole" into a number (say y) of equal (in some sense) parts,
3) we state the number (say x) of those equal parts being considered.

The symbol, x/y, is assigned to the result of this process. For example, in the figure below, we took the "whole",
which is the larger outer rectangle, and divided it up into 8 equal parts and we shaded (considered) 5 of these
parts. The result is that we have 5 eighths of the whole, which is written symbolically as 5/8. The following is an
example of an area model, representing 5/8.

xxxxxxxxxxxxxxx	xxxxxxxxxxxxxxx
xxxxxxxxxxxxxxx	xxxxxxxxxxxxxxx	xxxxxxxxxxxxxxx

Example 1:

In the figure below, why is it incorrect to say that 1/3 of the rectangle is shaded?

xxxxxxxxxxx xxxxxxxxxxx

Solution : We took the large rectangle and divided it into three regions or parts, one of the
three regions is shaded. The problem is that the regions are not equal. When we
look at a fraction like 1/3, we are assuming that the "whole" has been divided into three
equal parts.

**********************************************************************************************************************************
**

Now You Try (Section 2.1)

1) Divide the rectangle into 3 congruent parts and shade 2 of the parts.

2) Divide the rectangle into 4 congruent parts and shade 3 of the parts.

3) Divide the rectangle into 6 congruent parts and shade 4 of the parts.

4) What fractions do each of the shaded regions represent in parts a - c?
1) _____ 2) _____ 3) _____

(Answers to Now You Try (Section 2.1) are found on page 28.)
**********************************************************************************************************************************
**

The following example illustrates the set model for fractions.

Example 1:

Divide the set of counters below into 3 equal parts and take 2 of these subsets. In this
case the "whole" is represented by the complete set of counters. What fraction of the
whole is represented?

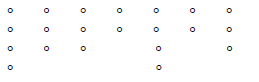
Solution: Since there are a total of 21 counters and we want to divide them up into 3 equal parts
each equal part will have 21 ÷ 3 or 7 counters.

The fraction represented is 2/3.

**********************************************************************************************************************************
**
Now You Try (Section 2.2)

1) Divide the set of counters below into 4 matching subsets and take 2 of these subset.

° ° ° °
° ° ° °
° ° ° °

2) Divide the set of counters below into 5 matching subsets and take 3 of these subsets.

° ° ° °
° ° ° °
° °

3) Divide the set of counters below into 7 matching subsets and take 2 of these subsets.

4) What fractions are represented in parts a - c?
1) _____ 2) _____ 3) _____
(Answers to Now You Try (Section 2.2) are found on page 28.)
**********************************************************************************************************************************
**

Example 2:

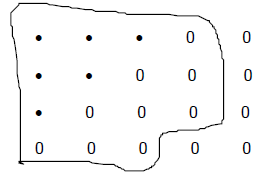
The shaded dots have a value of 2/5. Draw a circle around the "whole" or "1".

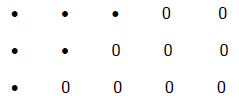
Solution: Since we have 6 shaded dots and the 2 in the numerator tells us that we have 2 equal
subsets, each subset would have to have 3 shaded dots in it. The 5 in the denominator
tells us that there are 5 subsets, this means that the "whole" would be represented by 15
dots (5 subsets with 3 dots each).

Another method to solve this problem would be to use a proportion

1) Count how many shaded dots are given. In this case, there are 6.
2) Make a proportion with the original fraction on the left and 6/x on the right

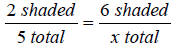
3) Solve the proportion by first cross multiplying .

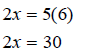
4) Then, divide both sides of the equation by 2.

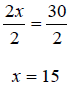
Therefore, there are 15 total dots that need to be circled.

In a previous course , you may recall a question such as, " 2/5 of what number is 6?". Example 2 above is really
asking you the same thing, the "whole" we are looking for in the example is the "number" you were looking for in
the question.

Example 3:

4/7 of what number is 8?

Solution: This question is asking you to find the "whole" if the 8 shaded dots represent 4/7

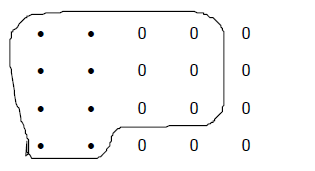
The 8 shaded dots have to be divided into 4 equal subsets, so each subset will have 2
dots. In the "whole" there are 7 subsets, so the "whole" will have 14 dots. Hence,
4/7 of 14 is 8.

We could also use a proportion to solve:

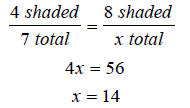
Therefore, 4/7 of 14 is 8.

**********************************************************************************************************************************
**

Now You Try (Section 2.3)

1) The shaded dots represent 5/7. Draw a circle around the "whole" or "1".

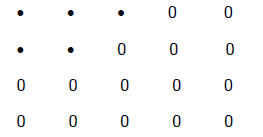
2) The shaded dots represent 3/5. Draw a circle around the "whole" or "1".

(Answers to Now You Try (Section 2.3) are found on page 29.)
**********************************************************************************************************************************
**

The following example illustrates the length or measurement model.

Example 1:

If we take a line segment (the whole or one) and divide it up into 8 equal parts and then
we consider 3 of those equal parts, the result is that we have 3 eighths, which is written
symbolically as 3/8.

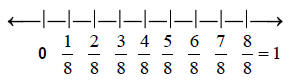
Example 2:

Given the following number line, state what fraction A represents.

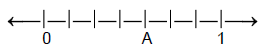
Solution: Since there are 7 equal parts from 0 to 1, each tic mark represents 1/7. So A = 4/7.

**********************************************************************************************************************************
**
Now You Try (Section 2.4)

1) Given the following number line, what fractions are represented by the letters A, B, C, and D?

2) Given the following number line, what fractions are represented by the letters A and B?

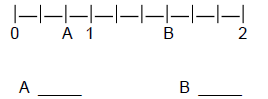
3) Approximate fractions represented by the letters A and B.

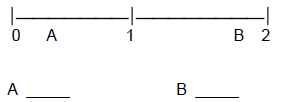
(Answers to Now You Try (Section 2.4) are found on page 29.)
**********************************************************************************************************************************
**