Functions and Inverse Functions
Asterisks denote definitions which are not in the
textbook.
1. We review the definitions leading up to the textbook's definition of inverse
function.
(a) *A relation is a set of ordered pairs .
(b) If there are sets R, A, and B such that
R ⊆ A × B,
then R is said to be a relation between A and B.
(Clearly, if R is a relation between A and B, then R is a relation as defined in
(a).)
(c) *The domain of a relation R, denoted by dom(R), is defined by
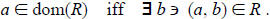
(d) *A relation R is called a function, or is said to have the function
property , iff
∀ a, b, c, and d, if (a, b) ∈ R and (c, d) ∈ R and a = c, then b = d.
In other words, a relation R is a function iff
if (a, b) ∈ R and (a, d) ∈ R then b = d.
(e) Given sets A and B, a relation F is said to be a function from A to B
iff
F is a relation between A and B;
F has the function property ;
dom(F ) = A (note that the fact that F is a relation between A and B implies
that ran(F) ⊆ B ).
The notation F : A → B means that F is a function from A to B, although the
exact verbal
interpretation of the symbols F : A → B may differ slightly depending on the
context.
(f) Theorem. *For a function F : A → B, define the relation F-1 by
(I) (b, a) ∈ F-1 iff (a, b) ∈ F , (I)
(i.e.,
z ∈ F-1 iff ∃ a, b 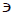 z = (b, a) and (a, b) ∈
F )
z = (b, a) and (a, b) ∈
F )
If the function F : A → B is bijective, then F -1 is a
function from B to A. (You should be
able to prove this.)
(g) The definition of inverse function given in the textbook can be expressed in
the following way:
If a function F : A → B is bijective, then the function F-1: B → A
defined above is called the
inverse function of F : A → B.
*To distinguish this concept from another inverse function concept discussed
below, we will
temporarily refer to this as the L-inverse function of F : A → B.
(The letter “L” refers to the author of the textbook.)
*I.e., a function G : B → A is the L-inverse function of a bijective function F
: A → B iff
dom(G) = B and G is the inverse relation F-1 of the relation F as defined in
(I) above.
(h) *Expressed in standard function notation instead of with the use of ordered
pairs , equation (I)
above gives the following defining condition for the L-inverse:
For every a in A and b in B ,
(I') F-1(b) = a iff F(a) = b.
We will give another definition of “inverse function”, and
then we will comment on the definitions and
the relationships between them.
2. *Given a function f : A → B, a function g : B → A is called an inverse
of the function f : A → B
iff
∀ x in A, g (f (x)) = x,
and
∀ y in B, f (g (y)) = y.
We will temporarily refer to such a function g : B → A as an
algebraic -inverse function of
f : A → B .
It should be clear that this definition is equivalent to the following :
For any set S, let idS denote the identity function on S.
Given a function f : A → B, a function g : B → A is called an
( algebraic -)inverse of the
function f : A → B iff
g o f = idA
and
f o g = idB .
Comments:
Uniqueness. It is clear that the L-inverse of a function is unique, if it
exists, since the L-inverse
function is obtained in a particular way from the original function. On the
other hand, if the inverse
function is defined as an algebraic -inverse, then it has to be proved that if
such an inverse function
exists, then it is unique.
Equivalence of L- inverse and algebraic -inverse. You should be able to
prove (this is related to
Ex. 7.29 in the textbook) that the L-inverse idea and the algebraic -inverse idea
are equivalent in the
following sense:
A function f : A → B has an algebraic -inverse function iff f : A → B is
bijective.
A function g : B → A is the L-inverse function of f : A → B iff g : B → A is an
algebraic -inverse
function of f : A → B.
Uniqueness. Note that this implies that if an algebraic-inverse function
exists, then it is unique.
| Prev | Next |