GEOMETRY EXAMINATION
INSTRUCTIONS
This test consists of 50 multiple choice questions. The
questions have not been arranged in order of difficulty .
For each question, choose the best of the five answer choices labeled A, B, C,
D, and E.
The test will be scored as follows: 5 points for each
correct answer, 1 point for each question left unanswered,
and 0 points for each wrong answer. (Thus a “perfect paper” with all questions
answered correctly earns a
score of 250, a blank paper earns a score of 50, and a paper with all questions
answered incorrectly earns a
score of 0.)
Random guessing will not, on average, either increase or
decrease your score. However, if you can eliminate
one of more of the answer choices as wrong, then it is to your advantage to
guess among the remaining
choices.
• All variables and constants , except those indicated
otherwise, represent real numbers.
• Diagrams are not necessarily to scale.
We use the following geometric notation:
| • If A and B are points, then: | • If A is an angle, then: |
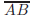 is the segment
between A and B is the segment
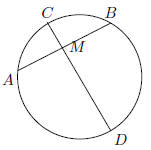
between A and B |
m∠A is the measure of angle A in degrees |
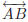 is the line
containing A and B is the line
containing A and B |
• If A and B are points on a circle, then: |
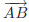 is the ray
from A through B is the ray
from A through B |
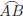 is the arc
between A and B is the arc
between A and B |
| AB is the distance between A and B | m 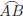 is the
measure of is the
measure of 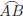 in degrees in degrees |
What You Can Do With A Mathematics Major
Occupational opportunities
| Actuarial and Insurance | Government | Accountant |
| Computer & Information Sciences | Investment Analyst | Financial Planner |
| Researcher | Benefits Specialist | Mathematician |
| Demographers | Computer Programmer | Cartographer |
| Data Processor | Navigator | Meteorologist |
| Applications Programmer | Ecologist | Health |
| Systems Analyst | Biomedical Engineer | Bio-mathematician |
| Computer Applications Engineer | Operations Analyst | Operations Research |
| Control Systems Engineer | Control Systems Engineer | Systems Engineer |
| Numerical Analyst | Teaching | BusinessIndustry |
| Statistician | Engineering Analyst | Financial Analyst |
| Technical Writer | Homeland Security | Communications Engineer |
Study in the field of mathematics offers an education with
an emphasis on careful problem analysis, precision
of thought and expression , and the mathematical skills needed for work in many
other areas. Many
important problems in government, private industry, health and environmental
fields, and the academic
world require sophisticated mathematical techniques for their solution . The
study of mathematics provides
specific analytical and quantitative tools, as well as general problem- solving
skills , for dealing with these
problems. The University of Alabama offers undergraduate and graduates degrees
in Mathematics.
Engineering Math Advancement Program
The University of Alabama is offering a new summer program
to build math skills for students entering engineering.
The Engineering Math Advancement Program (EMAP) is a summer residence class that
addresses
math and engineering prerequisites for incoming engineering students. The
program targets bright students
who may not have retained the information learned in high school and provides
and opportunity to hone
technical abilities before entering college. The goal of E-MAP is to assisting
entering freshmen in developing
a solid background in calculus to succeed in engineering before they start at
the University.
Classes are designed around Precalculus Algebra and
Trigonometry and incorporate important learning principles
to ensure that knowledge is retained and not just memorized. Students develop
their skills through
hands-on experiences, problem solving teaming exercises, and interaction with
engineering professors and
instructors through an interdisciplinary Living Laboratory program. Experiments
allow students to use simple
calculus in engineering applications. The program also involves introducing
students to local practicing
engineers through work on one or more community service engineering-related
activities. E-MAP will reserve
33-40 percent of enrollment space for underrepresented groups. Financial
assistance is available based on
need.
1. In a right square pyramid all five faces have the same
area. If the height of the pyramid is 9in, what
is the total surface area in square inchs ?
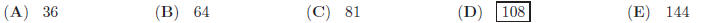
2. Two regular polygons of the same number of sides have
sides 48m and 55m in length respectively.
What is the length of the side of the another regular polygon of the same number
of sides, if its area
is equal to the sum of the two ?
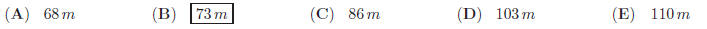
3. A 160 ft rope is suspended at its two ends from the top
of the 100 ft poles. If the lowest point to
which the midpoint at the rope can be polled from the ground is 72 ft, what is
the distance between
the poles ?

4. A circle with center O has a chord AB equal in length
to the radius of 1. A perpendicular from O to
AB meets AB at M. A perpendicular from M to OA at D. What is the area of
triangle AMD (in
unit square) ?
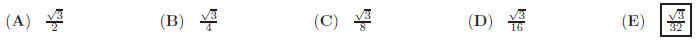
5. In the circle shown, AB = 24, and the perpendicular
chord 
How long is  is 4 times as long as
is 4 times as long as

6. If the diameter of a cylindrical can is increased by 30
percent, by approximating what percentage
should the height be increased to triple the volume of the can ?
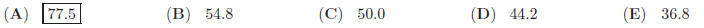
7. Find the circumference of a circle inscribed in an isosceles right triangle with legs of 1 .
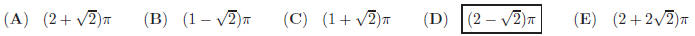
8. In the figure shown, ∠ADE = 100◦ and DE = DC = CB = BA.
What is the measure of ∠EAD?
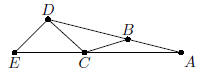
9. What is the length of the hypotenuse of a right
triangle that has an area of 40 and its longest leg has
length b ?
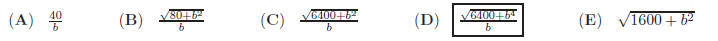
10. In the rectangular prism shown, the area of the faces
are 18, 40 and 80
respectively. What is the length of the diagonal
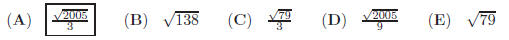
11. Find the possible values of k so that two lines kx+y = 3 and x−y = 2 intersect in the first quadrant .
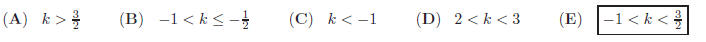
12. A circle is inscribed in a triangle with sides length
of 4 cm, 13cm and 15 cm. Find the area of the
circle .
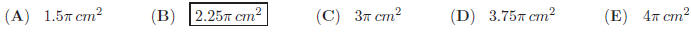
13. How many faces does a polyhedral solid with 36 vertices and 64 edges have ?
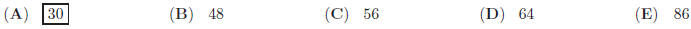
14. A cylindrical tank has a spiral staircase one foot
wide attached to its exterior. The staircase goes
from the bottom to the top while making exactly 4 complete revolution if the
tank is 20 ft high and
has a diameter of 16 ft. What is the length of the exterior edge of the
staircase (in feet) ?
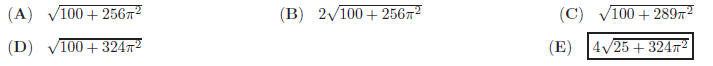
15. Find the radius of a circle if the difference between
the area of the inscribed and circumscribed
equilateral triangles is 25 square inches .
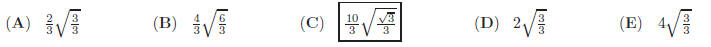
16. Find the area of a trapezoid in which the bases are 17m and 42m and the legs are 15m and 20m.
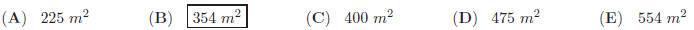
17. The sides of a triangle are the roots of
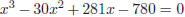 , and they are all natural numbers.
, and they are all natural numbers.
What is the area of the triangle (in unit square) ?
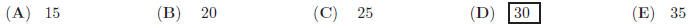
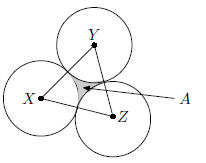
18. Three circles of equal radius
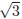 all touch each other to enclose a
all touch each other to enclose a
three cornered concave area A, which is shaded in the figure shown.
What is the area of A?
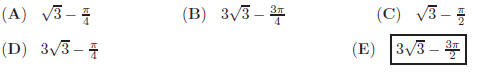
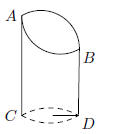
19. Given the cylinder as shown, which is cut on a slant.
The height goes from 15 in to
21 in, and the radius is 4in. Find the volume of the cylinder .
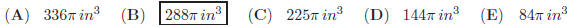
20. If ABCD is a square with E on DC such DE = 2 and EC =
4, then the perimeter of triangle AEB
is:
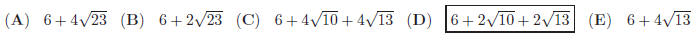
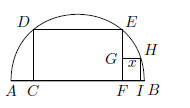
21. In the figure shown, A semicircle has diameter AB.
Rectangle CDEF is
inscribed in the semicircle with CD = 24 and DE = 56. Square FGHI
with side x is between the rectangle and the semicircle as shown. What
is the area of FGHI ?
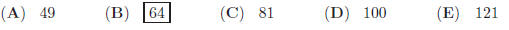
22. The length, width, and the height of a rectangular
solid are in the ratio of 6 : 8 : 24. If the diagonal
of the solid is 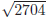 inches long, what is the
length of longest side of solid (in inches) ?
inches long, what is the
length of longest side of solid (in inches) ?
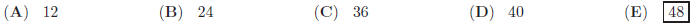
23. In the figure shown, the rectangle has a width of 6
and height of 5. Circle A has
radius r and circle B has radius 1. Find the value of r .
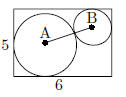
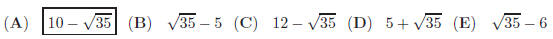
24. The center of the circle defined by
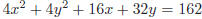 is (h, k). What is the product of h
is (h, k). What is the product of h
and k ?
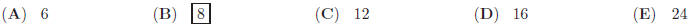
25. AB and CD are perpendicular to a diameters of circle
O. Let CM be a chord that intersect AB at
E, so that CE = 6 and EM = 5. Find the circumference of the circle .
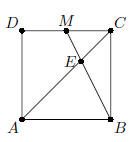
26. Given the square ABCD with M the midpoint of DC. The
ratio of the area
of the triangle MEC to that of the quadrilateral AEMD is:

27. Determine the area that is outside the square |x| + |y| ≤ 1 and inside the circle x^2 + y^2 = 1.
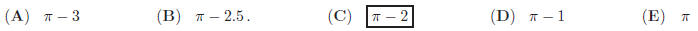
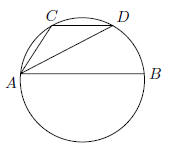
28. AB is a diameter of a circle and CD is a chord
parallel to AB. Find the
angle ∠C − ∠D:
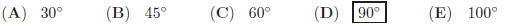
29. The side of a square is a. Find the length of a side
of a regular octagon
obtained from the square by cutting off its corners .
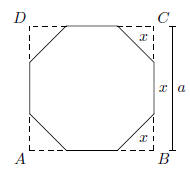
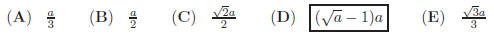
30. In the figure shown,
 are diameters of the given circle,
intersecting
are diameters of the given circle,
intersecting
on the center C of the circle. Also, F is the midpoint of the minor
arc determined by points A and D, and the chord
 intersects
intersects
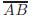 on
on
the point G. If ∠BCE has measure 60◦, then the measure of ∠AGF is:
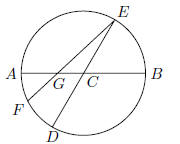

31. In the figure shown,
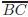 is tangent to the circle centered at the
origin.
is tangent to the circle centered at the
origin.
If  intersects the circle at
intersects the circle at
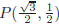 , then the length of the
, then the length of the
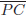 is:
is:
32. Sam sees that the top of a 15 foot lamp, which is 250
feet away, lines up perfectly with the peak of a
distant mountain. Sam knows that the mountain is 15 miles away so he uses the
lamp to determine
the height of the mountain. If Sam’s eyes are 5 feet above the ground, what is
the best estimate of
the height of the mountain relative to Sam?
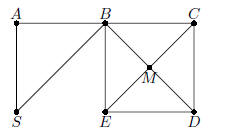
33. In the figure shown, how many different paths are
there from S to E
if one never visits the same point twice ?
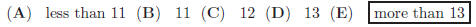
34. In the figure shown, six similar triangles are each
sharing
one side with the next triangle and all are sharing one
vertex. All angles at that vertex measure 60◦. If the
side of the last (smallest) triangle that is adjoining the
first triangle is 1/6 as large as the longest side of the
first triangle, how many times larger is the area of the
largest triangle as compared to the smallest ?
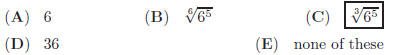
35. Find the height of a square pyramid formed by four
equilateral triangles
whose sides all have length 2 .
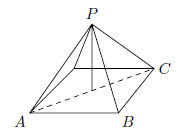
36. In triangle ABC, the measure of angle A is twice the
measure of angle B and the measure of angle
B is three times the measure of angle C. The measure of angle B is:
(A) less than 60◦
(B) at least60◦ but less than 65◦
(C) atleast65◦ but less than 70◦
(D) at least70◦ but less than 75◦
(E) atleast75◦
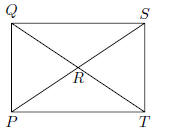
37. In the figure shown, the area of rectangle PQST is 9
square inches. If the
degree measure of ∠PRQ is 60◦, the length of side PQ (in inches) is:
38. Let A be the point (3, 2), and B be the reflection of
A about the x-axis. Let C be the reflection point
of B about the line y = −x and D be the reflection point of C about the origin.
what is the area of
the quadrilateral ABCD?
(A) 14 (B) 15 (C) 16 (D) 17 (E) 18
39. A and B are two points on the circle of radius r and
center O. If the distance between A and B is r,
what is the radian measure of ∠AOB ?
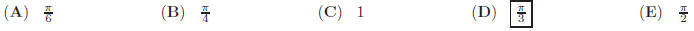
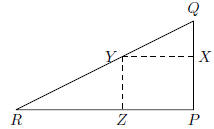
40. In the figure shown, PQR is a 3−4−5 right triangle
with right angle
at P. Points X, Y , Z on PQ, QR, PR respectively are chosen so
that PXY Z is a square. What is the length of the segment PX ?
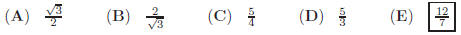
41. Given a right triangle with right angle at point C and
legs of length a and b, the length of the
segment which joins C to the hypotenuse of the triangle and which bisects the
angle at C is given by
the formula:
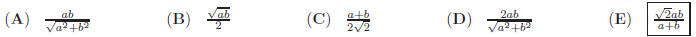
42. Equilateral triangle ABC has vertices A, B and C, and
center D. A new triangle A'B'C is formed
where A' is the midpoint of AD, B' is the midpoint of BD, and C' is the midpoint
of CD. The ratio
of the area of triangle ABC to the triangle A'B'C is :
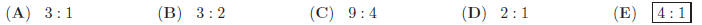
43. Let C be the circle described by (a − x)^2 + y^2 = r^2
where 0 < r < a. Let m be the slope of the line
through the origin that is tangent to C at a point in the first quadrant. Then
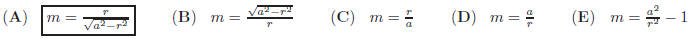
44. In  and the medians
to sides
and the medians
to sides  are perpendicular. Find
are perpendicular. Find
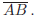

45. In a three dimensional rectangular coordinate system ,
find the total surface area of the solid defined
by | x | + | y | + | z |≤ 1 .
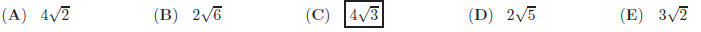
46. If the graphs of 2y + x + 3 = 0 and 3y + ax + 2 = 0 are to meet at right angle, then a is
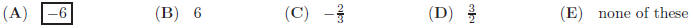
47. A pair of opposite vertices and the midpoints of a
pair of opposite edges of a cube are connected to
form a quadrilateral. If each edge of the cube has length k, find the area of
the quadrilateral.
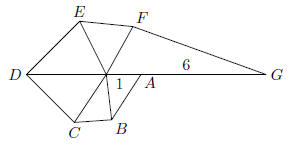
48. You have 6 sticks of lengths 10, 20, 30, 40, 50 and 60
centimeters. The number of non-congruent
triangles that can be formed by choosing three of the sticks to make the sides
is
(A) 3 (B) 6 (C) 7 (D) 10 (E) 12
49. A glass box of 7cm×12 cm× 18 cm, closed on all six
sides, is partly filled with colored water. When
the box is placed on one of its 7 × 12 sides, the water level is 15 cm above the
table. If the box is
placed on one of its 7 × 18 sides, what is the water level above the table, in
centimeters ?
(A) 7.5 (B) 9 (C) 10 (D) 10.5 (E) 11
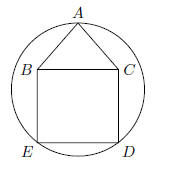
50. In the figure shown, ABEDC is circumscribe a circle
through points A, D
and E. ABC is an equilateral triangle with side length 2, and BCDE is a
square. Find the radius of the circle .
| Prev | Next |