Long Division of Polynomials
Long division of polynomials is very similar to long
division of numbers (most likely you didn’t
learn short division of numbers ). Anyway, you look at the first term of the
divisor and divide it into
the first term of the dividend .
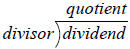 so in the case of ( y3 - y2
- 4y - 7)
so in the case of ( y3 - y2
- 4y - 7)
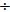 ( y +1)
( y +1)
you would divide y into y 3 resulting in y2 as shown.
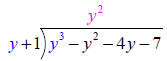 |
then multiply the quotient by the
divisor as in number division and place the result underneath in the appropriate columns. |
|
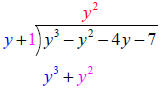 |
The next step is where a mistake is
often made, you need to subtract just as you would in number division. |
|
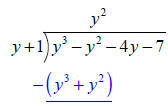 |
It is helpful here to distribute the minus sign, then add. | |
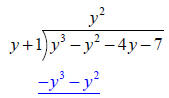 |
So that your result is | |
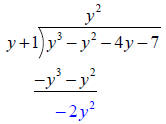 |
Now bring down the next term (as you
would bring down the next digit in number division) |
|
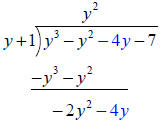 |
Now divide y into -2y2 to get -2y and multiply the quotient | |
| by the divisor as before. Remember
again you want to subtract . |
||
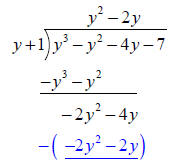 |
which gives you | 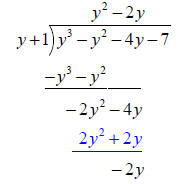 |
| Again, bring down the next term and divide . Multiply by quotient . | ||
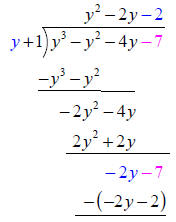 |
distribute the negative and add | 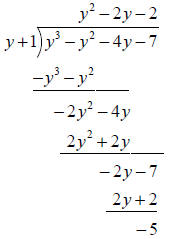 |
So that the quotient (answer) is: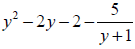 |
||
| Prev | Next |