Manipulating Fractions
The rules for manipulating fractions that involve algebraic expressions are
exactly the same
as the rules for manipulating fractions that involve numbers .
The fundamental rules for combining and manipulating fractions are listed
below. The uses
of these rules are illustrated more completely later in this appendix.
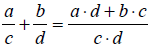
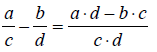
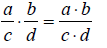
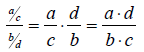
“Invert and multiply.”
Fractions express a ratio of two quantities . For example, the fraction
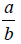
expresses the ratio of quantity a to quantity b. The quantity that appears on
the top of the
fraction is called the numerator. In this case, the numerator is a. The quantity
that appears
on the bottom of the fraction is called the denominator. In this case, the
denominator is b .
Finding a common denominator
Adding and subtracting fractions usually requires a common denominator, that
is, all of the
fractions involved have the same denominator.
Example E.1
Find common denominators for the following collections of fractions. Express
the
fractions using this common denominator.
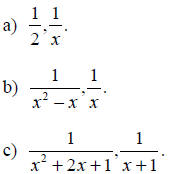
Solution:
a) The common denominator is 2x. The two fractions can be expressed by
multiplying
both numerator and denominator (top and bottom) by whatever factor is needed to
convert
the denominator to the common denominator.
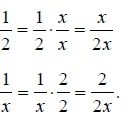
b) A common denominator can always be obtained by just multiplying each of
the
denominators together. A possible common denominator is
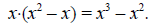
Expressing the two fractions using this common denominator:
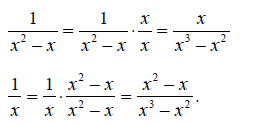
Note, however, that
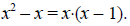The significance of this observation is that since x2 -
x already has the denominators of both
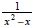and
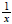as factors. So,
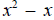is already a
common denominator for both of these fractions and could be used instead of
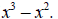
c) One way to obtain a common denominator is to just multiply the
denominators of the
two fractions
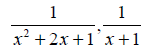
together. However, x2 + 2x + 1 = (x + 1)2. Since x + 1 is a factor of x2 + 2x
+ 1, x2 + 2x +
1 can be used as a common denominator. Expressing the two fractions using the
common
denominator x2 + 2x + 1:
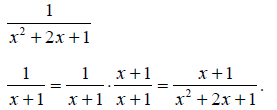
The advantage of using x2 + 2x + 1 as a common denominator (rather than, say,
the more
obvious (x + 1)×(x2 + 2x + 1) = x3 + 3x2 + 3x + 1) is that the fractions that
you obtain using
the common denominator are usually the simplest possible.
Adding and subtracting fractions
Fractions can only be added and subtracted when the two
fractions have the same
denominated. If the two fractions do not have the same denominator, then a
common
denominator must be found before the fractions can be added or subtracted. The
necessity
of finding a common denominator is why the product of the two denominators (i.e.
b×d)
appears in the rules expressed below. Expressed using algebraic symbols , the
rules for
adding and subtracting functions are:
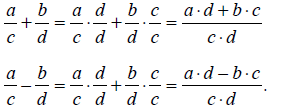
Example E.2
Evaluate and simplify each of the algebraic expressions.
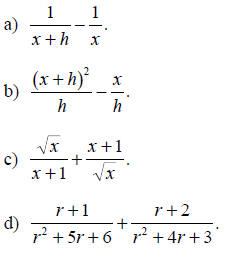
Solution:
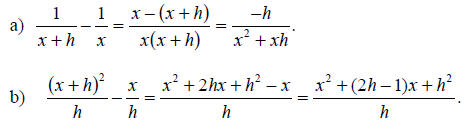
(The two fractions already have the same denominator.)
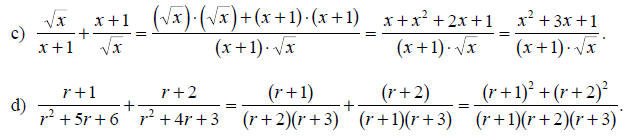
Some further simplifications are possible in Part (d). For
example, you could multiply out
all of the brackets . The important point in Part (d), however, is that by using
the simplest
(or “least”) common denominator, the algebraic form of the result will be as
simple as
possible. In the case of Part (d), the simplest common denominator is (r + 1)(r
+ 2)(r + 3),
rather than the more obvious common denominator (r + 1)(r + 2)(r + 2)(r + 3).
Multiplying fractions
Multiplying two fractions is perhaps the most
straight-forward of all operations. You
simply multiply the numerators and multiply the denominators. Expressed using
algebraic
symbols, this rule is:
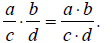
Example E.3
Evaluate and simplify the following fractions as much as possible
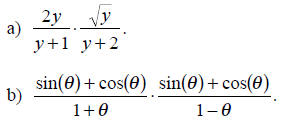
Solution:
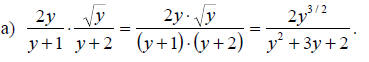
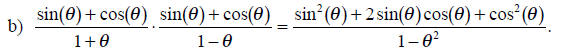
Dividing fractions
Many people remember the rule for dividing one fraction by another by
remembering that
you must “invert the denominator and multiply.” Expressed as algebraic symbols,
the rule
is:
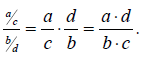
Example E.4
Evaluate or simplify each of the fractions given below.
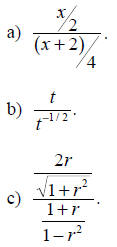
Solution:
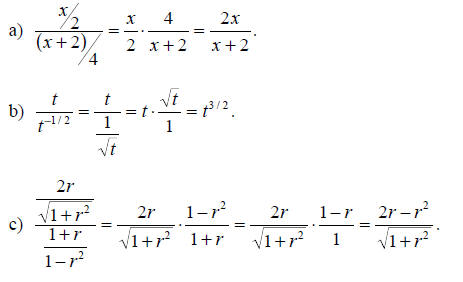
Simplifying complicated fractions
Sometimes, fractions will have other fractions in their
numerator or denominator (or both).
To simplify and evaluate complicated fractions, evaluate the numerator and
denominator
separately , and then divide the two.
Example E.5
Simplify each of the complicated fractions as much as possible.
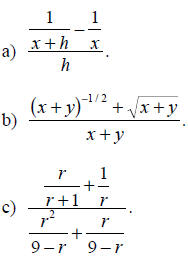
Solution:
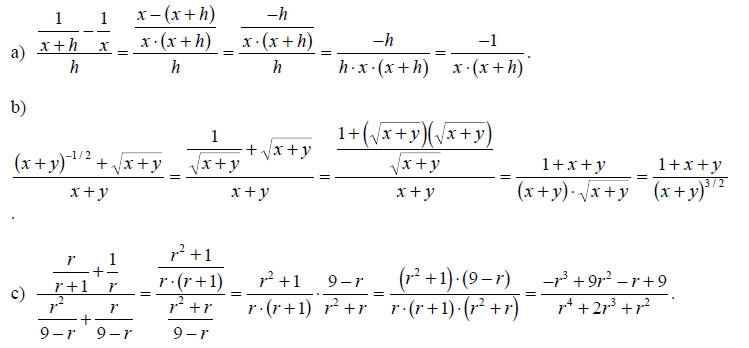
Exercises for Appendix E
For Problems 1-10, evaluate the quantity without using a calculator.
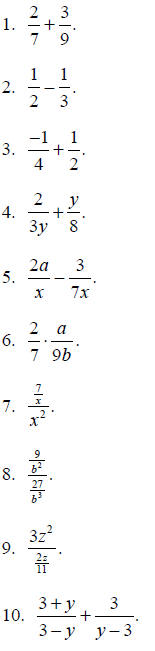
For Problems 11-20, perform the operation indicated .
Simplify your answers as much as
possible.
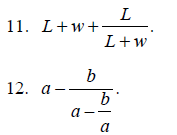
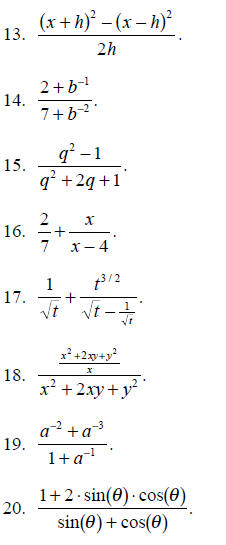
For Problems 21-25, decide whether each of the statements are true or false.
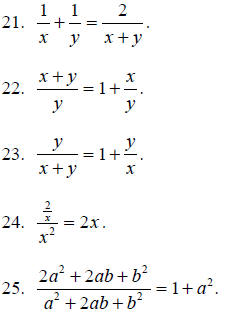
Answers to Exercises for Appendix E
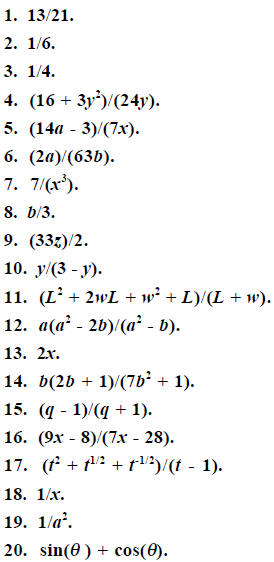
21. False.
22. True.
23. False.
24. False.
25. False.
| Prev | Next |