MATH 1105 Test 2
Show all work on test paper unless told otherwise.
All problems or parts of problems are 3 points
unless marked other wise.
Data dump Area:
Solve the system of equations by substitution.
1)
x + 4y = -17
4x + 3y = -3
Solve the system of equations by elimination .
2)
6x - 6y = 6
-2x - 2y = 2
Solve the problem.
3) A certain product has supply and demand functions given by p = 4q + 22 and
p = 457 - 11q, respectively, where p is the price in dollars and q is the
quantity supplied
or demanded at price p.
a) How many units are supplied and demanded at market equilibrium? (demand =
supply)
b) And what is the price of the units at market equilibrium?
Solve the inequality.
4)
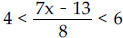
Solve the problem by writting an inequality and then
solving it. ( 4 pts)
5) Jim has gotten scores of 63 and 76 on his first two tests . What score must he
get on his
third test to keep an average of 70 or greater?
For problem 6: a) which way does graph open and why (
2pts)
b) is vertex minimum or maximum point ( 1 pt)
c) what is the vertex point ( 2 pts)
6) f(x) = -4x2 + 2x - 6
Write the vertex form of a parabola that satisfies the
given conditions. Then write the equation in
standard form of parabola. ( 4 pts)
7) Vertex (3, 4) and a = 4
Solve the problem.
8) At Allied Electronics, production has begun on the X-15 Computer Chip. The
total
revenue function is given by R(x) = 58x - 0.3x2 and the total cost
function is given by
C(x) = 9x + 9, where x represents the number of boxes of computer chips
produced. The
total profit function, P(x), is such that P(x) = R(x) - C(x).
a) Find P(x). ( 2pts)
b) How many units are needed to maximize the profit?
c) What is that maximize profit?
9) An object is thrown upward with an initial velocity of
14 ft per sec. Its height is given by
h(t) = -14t2 + 56t at time t seconds.
a) After how many seconds does it hit the ground?
b) How many seconds does it take it reach its maximum height AND what is that
height?
(5pts)
Use factoring to solve the equation.
10) 2x2 - 18x + 40 = 0
11) 3x2 - 20x = 7
Use the square root method to solve the equation.
12) x2 + 3 = 172
Use the square root property to solve the equation.
13) (x + 2)2 = 81
Use the quadratic formula to solve the equation.
14) p2 + 5p - 5 = 0
Find the solutions to the quadratic equation in the complex numbers ., by
using the quadratic
formula.
15) x2 + x + 4 = 0
Solve the problem. Make sure you show me your work.
16) A ball is thrown downward from a window in a tall building. The distance
traveled by
the ball in t seconds is s = 16t2 + 32t, where s is in feet. How long
(to the nearest tenth)
will it take the ball to fall 165 feet?
Solve the problem.
17) The function defined by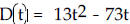 
gives the
distance in feet that a car going
approximately 50 mph will skid in t seconds. Find the time it would take for the
car to
skid 380 ft. Round to the nearest tenth.
18) At Allied Electronics, production has begun on the
X-15 Computer Chip. The total cost
function is given by C(x) = 4x + 10 and the total profit function is given by
P(x) = - 0.3x2 + 51x - 10, where x represents the number of boxes of
computer chips
produced. The total revenue function, R(x), is such that R(x) = C(x) + P(x).
a) Find R(x).
b) How many units are needed to maximize the revenue?
c) What is that revenue?
Graph ( shade) the solution region for the system of
inequalities and identify the corners of the
region. ( 6pts)
19)
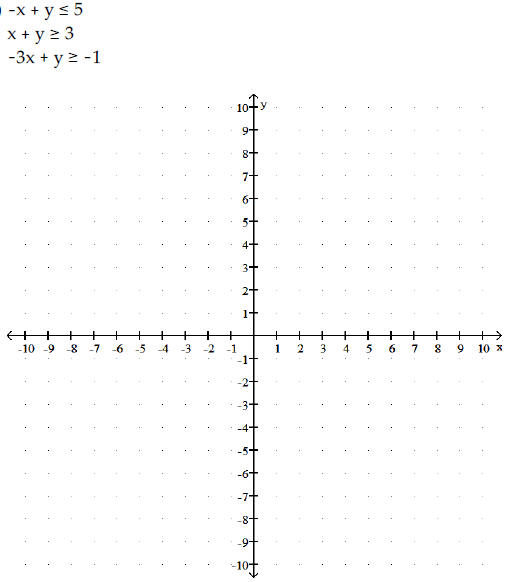
20) A company produce two types of printers, the Inkjet
and the Laserjet. It takes 4 hours to
make the Inkjet and 8 hours to make the Laserjet. The company can make at most
150
printers per day and has 800 labor-hours available per day. Let x represent the
number
of Inkjet printers produced in a day and y represent the number of Laserjet
printers
produced in a day.
a) Write a system of 4 inequalities to describe system. ( 6 pts)
b) Identify the corners(4) of the solution area. (you do not need to put graph
on test
paper, 4 points)
Write the system of 4 inequalities that describe the
problem. ( 6 pts)
21) The Acme Class Ring Company designs and sells two types of rings: the VIP
and the SST.
The company can produce up to 140 rings each day, using up to 350 total
man-hours of
labor. It takes 5 man-hours to make one VIP ring and 7 man-hours to make one SST
ring.
Let x represent the number of VIP rings, and let y represent the number of SST
rings.
These problems are extra credit, 2 points each. For a maximum of 5 points extra
credit.
Evaluate the function.
22)
Given f(x) = 6x - 8, find f(-16).
Write the equation of the line using the information given about its graph.
23) Slope -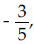
y- intercept (0, 8)
Write the slope -intercept form of the equation for the
line passing through the given pair of
points.
24) (-4, 7) and (0, -6)
Solve the equation.
25)
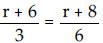
26) -6.1q + 1.0 = -43.1 - 1.2q
| Prev | Next |