18.100B Problem Set 1

Problems.

1) (10 pts) Prove that there is no rational number whose square is 12.

2) (10 pts) Let S be a non-empty subset of the real numbers , bounded above. Show that if
u = sup S, then for every natural number n , the number u − 1/n is not an upper bound of S,
but the number u + 1/n is an upper bound of S.

3) (10 pts) Show that if A and B are bounded subsets of R, then A∪B is a bounded subset of
R. Show that
supA ∪ B = max{sup A, supB}.

4) (20 pts) Fix b > 1.
a) If m, n, p, q are integers, n > 0, q > 0, and r = m/n = p/q, prove that

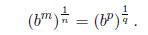
Hence it makes sense to define 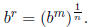(How could it have failed to make sense?)
b) Proce that b^r+s = b^rb^s if r, s are rational.
c) If x is real, define B (x) to be the set of all numbers b^t, where t is rational and t ≤ x.
Prove that
b^r = supB (r)

when r is rational . Hence it makes sense to define
b^x := supB (x)

for every real x .
d) Prove that b^x+y = b^xb^y for all real x and y.

5) (10 pts) Prove that no order can be defined in the complex field that turns it into an ordered
field.
(Hint: −1 is a square .)

6) (10 pts) Suppose z = a + bi, w = c + di. Define
z < w if a < c or a = c, b < d

Prove that this turns the set of all complex numbers into an ordered set. (This is known as a
dictionary order , or lexicographic order.) Does this ordered set have the least -upper-bound
property ?

7) (10 pts) Prove that
|x + y|² + |x − y|² = 2|x|² + 2|y|²

if x ∈ R^k and y ∈ R^k. Interpret this geometrically, as a statement about parallelograms.

Extra problems:
1) (Another argument showing that )
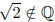Show that, if n² = 2m², then
(2m − n)² = 2(n − m)².

Deduce that, if n and m are strictly positive integers with n² = 2m², we can find strictly
positive integers n', m' with (n')² = 2(m')² and n' < n. Conclude that the equation
n² = 2m² has no non-zero integer solutions.

2) Show that the square root of an integer is either an integer or irrational.
(Hint: Every integer has a unique ( up to order ) factorization into a product of prime numbers,
you can use this to show that if n is an integer and a prime p divides n ², then p divides n.)