Math 20A Final Review Outline
Section 3.6: Trigonometric Functions
• Know the relationship between sine and cosine (in terms of derivatives ). The
following table
summarizes all of this nicely .
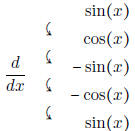
Also,
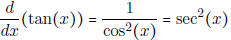
• Know how to use the quotient rule to find the derivative of other
trigonometric functions.
- 
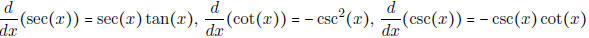
- What is the derivative of sin(ex) cos(2x)?
- What the slope of the tangent line of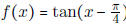 
at
?
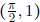Section 3.7: The Chain Rule
• Know the chain rule and how to apply it to solve problems.
Chain Rule: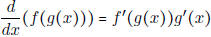 
.
- Find the derivative of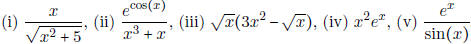 
.
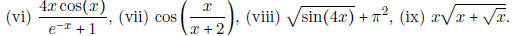• Know the generalized power rule and generalized exponential rule :
General Power Rule: 
. (Here, f(x) = xn and
g(x) = g(x).)
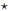General Exponential Rule: 
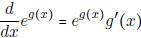. (Here, f(x) =
ex and g(x) = g(x).)
• Know how to find the equation of a tangent line using any of the above rules.
- Find the equation of the tangent line of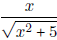 
,
at x = 2.
- Find the equation of the tangent line of y = sin(sin(x)) at the point (2π , 0).
• Given a table of data, know how to compute various
derivatives.
- Suppose f(1) = 2, f'(1) = 3, f(2) = 0, f'(2) = 1, g(1) = −1, g'(1) = 4, g(2) =
1, g'(2) = 5.
Compute (i) h'(1) if h(x) = f(x)g(x), (ii) h'(2) if h(x) = f(g(x)),
(iii) h'(1) if h(x) = [f(x)]2, (iv) h'(1) if h(x) = g(f(x)):
- Suppose that f(x) and g(x) are differentiable functions satisfying:
f(2) = 5, g(2) = 4, f'(2) = −3, g'(2) = 9,
f(4) = 3, g(4) = 2, f'(4) = −2, g'(4) = 3:
Find the derivative of each of the following functions at x = 2.
(i) G(x) = f(g(2x)) and (ii) H(x) = f(x2)g(x)
Section 3.8: Implicit differentiation
• Know how to find the derivative of a curve using implicit differentiation.
1. Take the derivative of both sides of the equation with respect to x.
2. Solve for y' by collecting the terms involving y' on one side and the
remaining terms on
the other side of the equation.
• Note: Remember, whenever you take the derivative of a function involving y,
you need to
multiply by y'. (The y' comes from the chain rule.) For example,
.
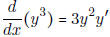- Find the derivative, y', to the curve ln(xy) = 3x.
- Consider the curve defined by the equation xy2 = cos(x) + sin(y). Find
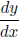and the
tangent line approximation at the point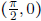 
.
- We wish to find all points where the graph of y 2 = x3 − 6x + 1 has a horizontal
tangent.
(i) Using implicit differentiation, find 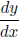. (ii)
Set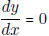 
and solve for x. This yields two
possible values of x . (iii) Show that one of the x values found in (ii) does not
correspond
to any point on the graph, but that the other value of x corresponds to two
points on
the graph. Find these points.
- The curve defined by the equation x2 + xy + y2 = 27 is an ellipse.
(i) Find y' using implicit differentiation. (ii) Find the point(s) on the curve
at which the
corresponding tangent line is horizontal.
Section 3.9: Derivatives of Inverse Functions
• Know how to find the derivative of the inverse
- If f(x) is differentiable and one-to-one with an inverse g(x), then for x such
that
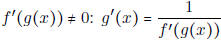
• Know the following derivatives (these are good to put on a cheat sheet...)
• Know the following derivatives (these are good to put on a cheat sheet...)
 |
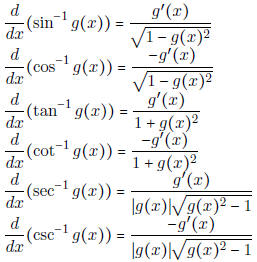[As a special case,  ] |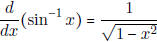
[As a special case,  ] |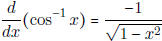
|
[As a special case,  ] |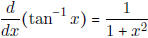
|
[As a special case,  ] |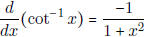
|
[As a special case,  ] |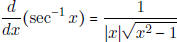
|
[As a special case,  ] |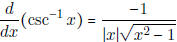
• Note: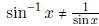 
! Rather, sin-1 x is the inverse of sin(x).
- What is the derivative of (i) f(x) = arcsin(x2) and (ii) g(x) = arctan(e3sinx)?
Section 3.10: Derivatives of General Exponential and
Logarithmic Functions
• Know that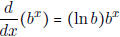 
- A special case is b = e.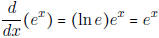 
.
- Find the derivative of (i)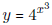 
and (ii) y = 52x
• Know the following derivatives (these are good to put on a cheat sheet...)
 |
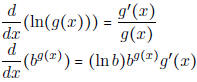[As a special case,
 ] |
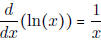[As a special case,
 ] |
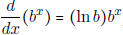- What is the derivative of f(x) = ln 23sinx?
- What is the second derivative of g(x) = 11sin(x)?
• Know how to find the derivative of the logarithm to another base
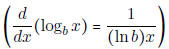
- Find f''(x) if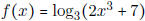 
• Know how to use logarithmic differentiation to find the derivative of f(x).
- Use logarithmic differentiation to compute the derivative of
.
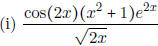• Know the following list of derivatives of hyperbolic functions
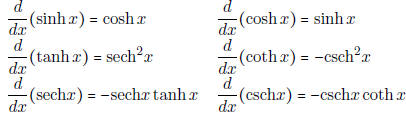
• Know the following list of inverse hyperbolic functions and their derivatives
| Function | Domain | Derivative |
 |
||
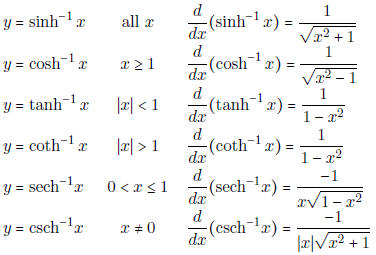Section 3.11: Related Rates
• Know how to identify a related rates problem.
- We have two or more variables and are asked to compute the ROC of one of the
variables
in terms of the ROCs of the other variable(s)
• There is no algorithm for solving these types of problems, which can make them
difficult to
start. Whenever possible, draw a diagram to illustrate how the variables are
related.
• Here is a general strategy:
1. Determine the variables involved in our scenario.
2. Find some formula that relates the variables.
3. Implicitly differentiate all variables with respect to time.
4. Plug in the quantities you know and solve for the unknown.
• Note: Step 2 is the most difficult. The two facts from geometry that come up the
most are
the Pythagorean Theorem and similar triangles (the ratio of corresponding sides
are equal).
- A spherical cell is growing at a constant rate of 400 μm3 (1 μm = 10-6m). At
what rate
is its radius increasing when the radius is 10 μm?
- The volume of a cube is increasing at a rate of 1cm3/min. How fast is the
surface area
increasing when the length of an edge is 2 cm?
- A 6 foot ladder stands leans against a wall. The foot of the ladder moves
outward at a
speed of 0.5ft/sec when the foot is 2 feet from the wall. At that moment, how
fast is the
top of the ladder falling?
- A particle moves along the x-axis from the point (0, 0) toward the point (4,
0) in the
xy-plane at a rate of 2 cm/sec. At what rate is the particle's distance to the
point (4, 4)
changing when it is halfway between the origin (0, 0) and the point (4, 0)? Be
sure to
clearly indicate whether the rate of change of the particle's distance to (4, 4)
is positive
or negative .
- A paper cup has the shape of a cone of height 12 cm and radius (at the top) of
3 cm. If
water is poured in at the rate of 8cm3/sec, how fast is the water level rising
when it is
5 cm deep? The volume of a cone with height h and radius r is
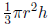
| Prev | Next |