Linear Independence and the Wronskian
Two functions , f and g are said to be linearly dependent on the interval
I if
there exists two constants k1 and k2 both non-zero such that:
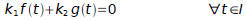(For all t that exist in the interval I)
Two functions , f and g are said to be linearly independent on the interval I if
there exists two constants k1 and k2 such that:
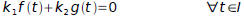
only when:
k1=k2=0
Example 1:
Is
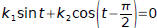linearly independent or linearly dependent?
The given functions are linearly dependent on any interval, since:
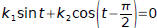
for all t if we chose:
k1=1 and k2=−1
Example 2:
Show that the functions
et and e2t
are linearly independent on any interval.
For t∈I must show that
k1=k2=0
Choose two points t0, t1∈I where t0≠t1
We suppose that
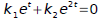
Evaluate this equation at these points.
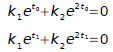
Evaluate the determinant of coefficients
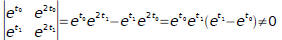
Since the determinant is not zero, the only possible solution is
k 1=k2=0
Theorem 3.3.1: If f and g are differentiable functions on an open interval I,
and
if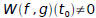 
for some point t0 in I, then f and g are linearly
independent on I. Moreover, if f and g are linearly dependent on I, then
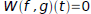for every t in I.
Theorem 3.3.2: (Abel's Theorem) If y1 and y2 are solutions of the differential
equation
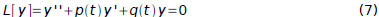
where p and q are continuous on an open interval I, then the Wronskian
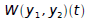is given by:
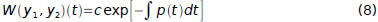
where c is a certain constant that depends on y1 and y2 but not on t.
Further,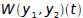 
either is zero for all t in I (if c=0 ) or else is never
zero in I (if c≠0 ).
Theorem 3.3.3: Let y1 and y2 be the solutions of Eq. (7)
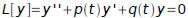
where p and q are continuous on an open interval I. Then y1 and y2
are linearly dependent on I if and only if 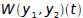is zero for all t in I .
Alternatively, y1 and y2 are linearly independent on I if and only if
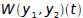is never zero in I.
Example 3:
Given
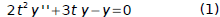
it was verified that
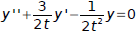
Verify that the Wronskian of y1, y2 is given by
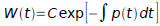
Equation 1 must be written in the form:
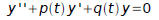
Equation 1 becomes :
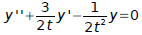
Therefore:
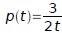and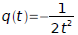 
Hence
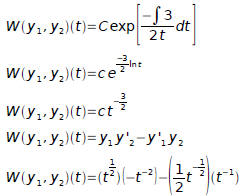
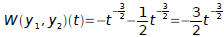It checks
| Prev | Next |